Système d'équations algébriques

[barbu23]

Bonsoir à tous,

On connait tous les méthodes de résolution des systèmes linéaire de type : , et que le système admet une unique solution lorsque la matrice associée à ce système est inversible.
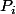
J'aimerai savoir dans quel cas un système algébrique de type : admet une unique solution avec : sont des polynômes à trois variables et ?

Merci d'avance. :happy3:

[chombier]

Bonsoir à tous,

On connait tous les méthodes de résolution des systèmes linéaire de type : , et que le système admet une unique solution lorsque la matrice associée à ce système est inversible.
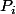
J'aimerai savoir dans quel cas un système algébrique de type : admet une unique solution avec : sont des polynômes à trois variables et ?

Merci d'avance. :happy3:

Surement pas dans le cas général, puisqu'avec une équation et une inconnue, on ne sait déjà pas résoudre une équation du type P(x)=0 si le degré du polynôme est supérieur ou égal à 5.

x^5 - 3 x -1 = 0 : on ne sait pas le résoudre.

[barbu23]

Merci chombier. :happy3:

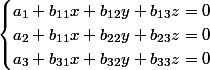
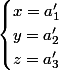
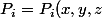Ce que je voulais dire, est que, pour moi, résoudre un système de type : ( ou un système de type : , c'est pareil ), consiste à le transformer en un système de type : ( ou un système de type : , c'est pareil ). La même chose pour un système algébrique : Pour moi, résoudre un système algébrique de type : avec : : polynômes de degré avec : , consiste à le transformer en un système de type : avec : , et : . 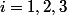Peux -t-on envisager une méthode pour trouver cette transformation ?

Merci d'avance.

[SLA]

Merci chombier. :happy3:

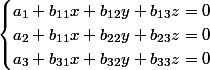
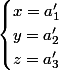
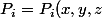Ce que je voulais dire, est que, pour moi, résoudre un système de type : ( ou un système de type : , c'est pareil ), consiste à le transformer en un système de type : ( ou un système de type : , c'est pareil ). La même chose pour un système algébrique : Pour moi, résoudre un système algébrique de type : avec : : polynômes de degré avec : , consiste à le transformer en un système de type : avec : , et : . 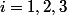Peux -t-on envisager une méthode pour trouver cette transformation ?

Merci d'avance.

Je vois difficilement l'intérêt d'une telle transformation, tu obtiendrais trois équations qui ne sont pas forcément soluble.
Enfin, pour ce qui est de l'étude des équations algébriques, les bases de Gröbner ont été inventées pour ça.
Cordialement

[barbu23]

Merci. Une base de Grobner, n'est elle pas une façon de déterminer une base d'un idéal de puisque ce dernier est noethérien ? Quel lien a cela avec le système d'équations algébriques que j'ai évoqué ?
Merci d'avance. :happy3:

[SLA]

Merci. Une base de Grobner, n'est elle pas une façon de déterminer une base d'un idéal de puisque ce dernier est noethérien ? Quel lien a cela avec le système d'équations algébriques que j'ai évoqué ?
Merci d'avance. :happy3:

C'est très simple: un ensemble algébrique engendré par une famille S de polynômes est le même que celui engendré par l'idéal . Ecris avec des symboles, ça donne:
où .

[barbu23]

C'est très simple: un ensemble algébrique engendré par une famille S de polynômes est le même que celui engendré par l'idéal . Ecris avec des symboles, ça donne:
où .

Ah d'accord, merci. Juste une petite question, la base de est-elle une base linéaire ou algébrique ?. Je ne connais rien en bases de Grobner pour être claire. :hum:
Et celui qui transforme des bases algébriques en bases algébriques sont des opérateurs tensoriels et non des opérateurs linéaires, non ? ça serait un peu dur, car on n'arrive pas à manier des tenseurs multidimensionnels, ça serait compliqué de les représenter spatialement comme une matrice. Y'a -t-il des méthodes de maniement de tenseurs d'ordre ? Je ne sais manier que des tenseurs d'ordre ( des matrices ).

[SLA]

Ah d'accord, merci. Juste une petite question, la base de est-elle une base linéaire ou algébrique ?. Je ne connais rien en bases de Grobner pour être claire. :hum:
Et celui qui transforme des bases algébriques en bases algébriques sont des opérateurs tensoriels et non des opérateurs linéaires, non ? ça serait un peu dur, car on n'arrive pas à manier des tenseurs multidimensionnels, ça serait compliqué de les représenter spatialement comme une matrice. Y'a -t-il des méthodes de maniement de tenseurs d'ordre ? Je ne sais manier que des tenseurs d'ordre ( des matrices ).

A quoi cela sert-il de te donner des références si tu ne prends pas le temps de regarder ce qu'on te donne?
Quelle distinction fais-tu entre base algébrique et base linéaire?

[barbu23]

A quoi cela sert-il de te donner des références si tu ne prends pas le temps de regarder ce qu'on te donne?
Quelle distinction fais-tu entre base algébrique et base linéaire?

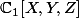
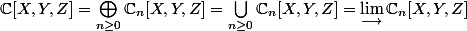
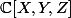
Une base linéaire est celle de dans , dont les éléments sont des formes linéaires ( projections ), et celle algébrique est celle de tout entier, dont les éléments sont de la forme : avec : sont des projections. ( C'est une base tensorielle ).
Je complique un peu l'explication, je sais. :ptdr:

[SLA]

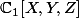
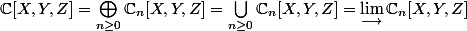
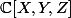
Une base linéaire est celle de dans , dont les éléments sont des formes linéaires ( projections ), et celle algébrique est celle de tout entier, dont les éléments sont de la forme : avec : sont des projections. ( C'est une base tensorielle ).
Je complique un peu l'explication, je sais. :ptdr:

Je ne suis pas sur de comprendre cette ligne . Que désigne ici ?

[Doraki]

Mon dieu, barbu comment tu fais pour ne pas comprendre qu'une réunion, une somme directe, et une limite inductive ce ne sont pas la même chose ? d'ailleurs ce sont des mots différents et des symboles différents ?

Sachant que dans aucun des 3 cas il y a un produit tensoriel (mais je suppose que tu as juste oublié de préciser que le produit tensoriel c'est pareil que la réunion, que la somme directe, et que la limite inductive)
quant à tes indices qui doivent vérifier i,j,k,...,l = x,y,z je sais vraiment vraiment pas à quoi tu penses quand tu écris qu'un triplet c'est un n-uplet pour n quelconque.

[SLA]

Mon dieu, barbu comment tu fais pour ne pas comprendre qu'une réunion, une somme directe, et une limite inductive ce ne sont pas la même chose ? d'ailleurs ce sont des mots différents et des symboles différents ?

Sachant que dans aucun des 3 cas il y a un produit tensoriel (mais je suppose que tu as juste oublié de préciser que le produit tensoriel c'est pareil que la réunion, que la somme directe, et que la limite inductive)
quant à tes indices qui doivent vérifier i,j,k,...,l = x,y,z je sais vraiment vraiment pas à quoi tu penses quand tu écris qu'un triplet c'est un n-uplet pour n quelconque.

Merci, ça me rassure! j'ai cru que j'avais tout oublié de mon cours de géométrie algébrique.

[barbu23]

Je m'excuse, je voulais écrire : avec : au lieu de .
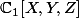
Donc, une base linéaire est la base naturelle ( "canonique" ) de qui vérifie ces conditions. Est ce que maintenant la suite de ce que j'ai dit dans le message précédent est correcte ?. Si ce n'est pas correcte, pouvez vous me corriger pour que ça devient correcte ?
Je sais que la limite inductive change de sens d'une catégorie à l'autre, mais, je ne sais pas à quelle catégorie elle correspond dans notre situation ? On est dans quelle catégorie là ?
Merci d'avance. :happy3:

[SLA]

Je m'excuse, je voulais écrire : au lieu de .
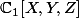
Donc, une base linéaire est la base naturelle ( "canonique" ) de . Est ce que maintenant la suite est correcte ?. Si ce n'est pas correcte, pouvez vous me corriger pour que ça devient correcte ?
Je sais que la limite inductive change de sens d'une catégorie à l'autre, mais, je ne sais pas à quelle catégorie elle correspond dans notre situation ? On est dans quelle catégorie là ?
Merci d'avance. :happy3:

Tu ne m'a toujours pas dit qui est .
Mais je soupçonne de ne pas être un espace vectoriel, ni anneau (0 n'est pas dedans, non?).
Quant à te corriger, je pense que vu la littérature qui existe sur internet, doublée de ta capacité à ne pas lire les références qu'on te propose, je vais te laisser te corriger tout seul.
Bon courage

[barbu23]

Excuse moi, j'ai corrigé. Regarde maintenant. :happy3:

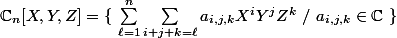
[barbu23]

Voiçi le poste corrigé :

Je m'excuse, je voulais écrire : avec : au lieu de .
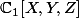
Donc, une base linéaire est la base naturelle ( "canonique" ) de qui vérifie ces conditions. Est ce que maintenant la suite de ce que j'ai dit dans le message précédent est correcte ?. Si ce n'est pas correcte, pouvez vous me corriger pour que ça devient correcte ?
Je sais que la limite inductive change de sens d'une catégorie à l'autre, mais, je ne sais pas à quelle catégorie elle correspond dans notre situation ? On est dans quelle catégorie là ?
Merci d'avance. :happy3:

[SLA]

Excuse moi, j'ai corrigé. Regarde maintenant. :happy3:

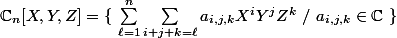
Quel est l'intérêt de la somme en 1 et n?
De plus dans , j'ai du mal à croire que soit dans le membre de droite, alors qu'il manifestement dans le membre de gauche (c'est la remarque de Doraki).
Bref qu'est-ce qu'une base linéaire (resp. base algébrique)?

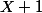
EDIT: pardon, j'ai mal lu. Mais c'est pas grave, ça retourne le problème: comment ta somme peut-elle être directe (encore une remarque de Doraki)? puisque est dans C1, C2, C3, etc

[barbu23]

Quel est l'intérêt de la somme en 1 et n?
De plus dans , j'ai du mal à croire que soit dans le membre de droite, alors qu'il manifestement dans le membre de gauche (c'est la remarque de Doraki).
Bref qu'est-ce qu'une base linéaire (resp. base algébrique)?

L'interet de la somme en et est qu'elle permet de construire un système inductive : ( des injections canoniques ) : , et donc, la limite inductive est la réunion des composants de cette suite, mais, je ne sais pas encore, s'il correspond à la sommation : . Est ce que c'est oui ?
Merci d'avance. :happy3:

[barbu23]

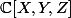
Une base linéaire dans est une base d'un espace vectoriel, une base algébrique est une base d'une algèbre graduée tensorielle. :happy3: C'est moi, qui a inventé ce terme pour exprimer ce que je cherche à te transmettre. Un espace vectoriel s'injecte dans une algèbre graduée tensorielle. :happy3:

[barbu23]

Pour moi, lorsqu'on écrit : avec : irréductible, alors, pour moi : est une base algébrique, et non, linéaire, par contre, est une algèbre graduée tensorielle avec : irréductible, et non un espace vectoriel ( extension ).