Système d'EDO
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 07 Oct 2012, 03:27
par barbu23 » 07 Oct 2012, 03:27
Bonjour à tous, :happy3:
Pourriez vous m'aider à résoudre le système suivant :
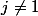
et
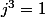
.
 \\ y'(t) \\ z'(t) \end{pmatrix} = \begin{pmatrix} 1 & 1 & 1 \\ 1 & j & j^2 \\ 1 & j^2 & j \end{pmatrix} \begin{pmatrix} x(t) \\ y(t) \\ z(t) \end{pmatrix} $)
Merci d'avance. :happy3:
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 07 Oct 2012, 07:38
par wserdx » 07 Oct 2012, 07:38
Il suffit de faire un changement de base qui diagonalise la matrice (qui est de Vandermonde pour

)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 07 Oct 2012, 17:33
par barbu23 » 07 Oct 2012, 17:33
Merci @wserdx.
Quel est le polynôme caractéristique de la matrice :

?
Merci d'avance. :happy3:
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 07 Oct 2012, 18:27
par wserdx » 07 Oct 2012, 18:27
- Code: Tout sélectionner
CharacteristicPolynomial[{{1, 1, 1}, {1, E^(((2 I)/3) Pi), E^(((-2 I)/3) Pi)}, {1, E^(((-2 I)/3) Pi), E^(((2 I)/3) Pi)}}, x]
Le polynôme cararctéristique :
- Code: Tout sélectionner
3/E^(((2 I)/3) Pi) - 3 E^(((2 I)/3) Pi) + 2 x - x/E^(((2 I)/3) Pi) - E^(((2 I)/3) Pi) x + x^2 + 2 E^(((2 I)/3) Pi) x^2 - x^3
- Code: Tout sélectionner
JordanDecomposition[{{1, 1, 1}, {1, E^(((2 I)/3) Pi), E^(((-2 I)/3) Pi)}, {1, E^(((-2 I)/3) Pi), E^(((2 I)/3) Pi)}}]
La matrice de changement de base et la matrice diagonale :
- Code: Tout sélectionner
{{{1 - Sqrt[3], 0, 1 + Sqrt[3]}, {1, -1, 1}, {1, 1, 1}}, {{-Sqrt[3], 0, 0}, {0, I Sqrt[3], 0}, {0, 0, Sqrt[3]}}}
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 07 Oct 2012, 18:38
par barbu23 » 07 Oct 2012, 18:38
Ce n'est pas la réduction de Jordan @wserdx, ce que je cherche, mais la diagonalisation. :hum: :lol3:
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 07 Oct 2012, 18:41
par wserdx » 07 Oct 2012, 18:41
Ben, dans ce cas là c'est pareil!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 07 Oct 2012, 19:00
par barbu23 » 07 Oct 2012, 19:00
Pourquoi, c'est pareil ? :mur:
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 07 Oct 2012, 19:04
par wserdx » 07 Oct 2012, 19:04
Parce que toutes les valeurs propres sont simples et distinctes.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 07 Oct 2012, 19:18
par barbu23 » 07 Oct 2012, 19:18
Ah d'accord, merci beaucoup. Si ce n'était pas diagonalisable, on fait une réduction de Jordan, et donc, on obtient une matrice diagonale par blocs, et là les valeurs

apparaissent.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités