Système de Cramer

[mehdi-128]

Bonsoir,

Soit le système d'équation suivant :




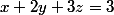
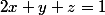
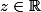
Afin de le résoudre, je ne comprends pas pourquoi on a le droit de fixer afin de se ramener au système de Cramer suivant :

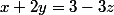
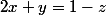
[Carpate]

Ce système d'équations comporte 2 équations pour 3 inconnues peut s'écrire matriciellement :
=
On voit qu'il n'est pas de Cramer car la matrice de gauche n'est pas inversible
Par contre en considérant z comme un paramètre et non une inconnue, le système s'écrit :
=
qui est bien un système de Cramer : solution unique dépendant du paramètre z

[chan79]

Bonsoir,
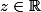
Afin de le résoudre, je ne comprends pas pourquoi on a le droit de fixer afin de se ramener au système de Cramer suivant :

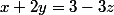
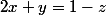
Salut
En fait, on exprime x et y en fonction de z qui varie dans
On peut ensuite remplacer z par k.
On arrive à une représentation paramétrique de droite. C'est celle qui passe par le point de coordonnées (-1/3;5/3;0) et qui est dirigée par le vecteur (1/3;-5/3;1)ou par (1;-5;3)

[mehdi-128]

Oui merci pour vos réponses, je trouve bien la même droite, de toute façon, comme les vecteurs normaux des 2 plans ne sont pas colinéaires, l'intersection des 2 plans est bien une droite.

Je trouve

Mais j'ai une question : on aurait pu fixé fixer x ou y au lieu de z ?

[chan79]

Mais j'ai une question : on aurait pu fixé fixer x ou y au lieu de z ?

Bien-sûr. Fais le calcul
Tu n'auras peut-être pas le même point mais tu auras un vecteur colinéaire. Ce sera la même droite.
C'est même plus simple en prenant x comme paramètre . On obtient le point(0;0;1), facile à vérifier avec les équations de départ.

[mehdi-128]

Ok merci.