Un système complexe

[fatal_error]

Bonjour Arbre,

cela fait un petit moment que nous trouvons ton comportement limite.
Je t'invite (grandement) à réfreiner tes interventions à but trollesque.

cdt,
fatal_error

[Arbre]

Bonjour,

Provocateur (avec certains), je veux bien, mais trollesque je ne suis pas d'accord.
Si ce n'est pas évident pour moi et que je ne suis pas convaincu, j'ai le droit de le dire, et d'expliquer pourquoi je ne suis pas convaincu, je ne vois pas en quoi cela est trollesque, c'est argument contre argument.

Ensuite utiliser le bannissement pour me bayonner, vous pouvez le faire, ce site est privé et donc il appartient à un particulier qui en fait ce qu'il veut.

Voilà.

[Dacu]

Bonjour,

Par exemple, en faisant c1=c2=0 dans les solutions trouvées, on obtient f'(x)=-i, g'(x)=1/3 et |f(x) +3ig'(x)| = |ix-3| (sauf erreur), et non pas ix-3.

Bonsoir,

Pour les deux premières fonctions f et avec on obtient:
pour et pour où et qui est parfaitement valide.

Q.E.D.

Tous les meilleurs!Cordialement,

Dacu

[zygomatique]

dacu = arbre = dattier = pourexemple = ... d nombreux bannissements de partout ...

[Dacu]

dacu = arbre = dattier = pourexemple = ... d nombreux bannissements de partout ...

Salut,

S'il vous plaît faire des calculs et voir que « WolframAlpha » a donné la réponse correcte!
Une machine est une machine ...mais l'homme conduit la machine....

Cordialement,

Dacu

[Arbre]

dacu = arbre = dattier = pourexemple = ... d nombreux bannissements de partout ...

Mon cher Gérard,

J'appelle cela de la diffamation, en effet tu m'accuses d'avoir plusieurs compte ici, ce qui n'est pas le cas et surtout qui est hors charte, hors le compte un_homme dont je ne retrouve pas le mot de passe, mais cela a été dit depuis l'ouverture de mon compte "Arbre".

Visiblement il n'est pas donné à tout le monde de deviner par le mode d'expression de chacun l'identité des uns et des autres.

Je pense que cela doit être monnaie courante chez vous (les gnostiques) de tels pratiquent, maintenant j'en arrive à me demander si ce site ne compte pas que 2 participants, toi et moi...

Voilà, voilà.

[Pseuda]

Bonjour,

Par exemple, en faisant c1=c2=0 dans les solutions trouvées, on obtient f'(x)=-i, g'(x)=1/3 et |f(x) +3ig'(x)| = |ix-3| (sauf erreur), et non pas ix-3.

Bonsoir,

Pour les deux premières fonctions f et avec on obtient:
pour et pour où et qui est parfaitement valide.Dacu

Bonsoir,

On obtient donc avec , ce qui donne , soit .
On en revient à la solution du début, avec f et g définies en un seul point, imaginaire pur, ce qui est doublement impossible pour des dérivées de fonctions de variable réelle.

Donc apparemment Wolfram ne vérifie pas que les solutions trouvées sont cohérentes avec les données du problème.

[Dacu]

Bonjour,

Par exemple, en faisant c1=c2=0 dans les solutions trouvées, on obtient f'(x)=-i, g'(x)=1/3 et |f(x) +3ig'(x)| = |ix-3| (sauf erreur), et non pas ix-3.

Bonsoir,

Pour les deux premières fonctions f et avec on obtient:
pour et pour où et qui est parfaitement valide.Dacu

Bonsoir,

On obtient donc avec , ce qui donne , soit .
On en revient à la solution du début, avec f et g définies en un seul point, imaginaire pur, ce qui est doublement impossible pour des dérivées de fonctions de variable réelle.

Donc apparemment Wolfram ne vérifie pas que les solutions trouvées sont cohérentes avec les données du problème.

Bonjour

Il n'est pas obligatoire que parce que ... et donc ."WolframAlpha" a donné les fonctions qui verifier le système , évidemment pour certaines valeurs complexes de .
Lire s'il vous plaît:

https://www.google.ro/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&uact=8&ved=0ahUKEwi3s8m95-7UAhXEJsAKHfwJAXsQFggrMAA&url=https%3A%2F%2Fwww.math.u-psud.fr%2F~pansu%2Fweb_ifips%2Fvarcomp.pdf&usg=AFQjCNF-qxspLU0A7kwYpC1zfyyFzRgXTg

et

https://fr.wikipedia.org/wiki/Analyse_complexe.

Tous les meilleurs!Cordialement,

Dacu

[Pseuda]

Bonjour,

Je ne connais pas l'analyse complexe, mais je ne vois pas très bien comment, les fonctions f, g et le complexe x vérifiant simultanément les 2 équations différentielles, impliquant 2 relations que doit vérifier x pour que ce système ait une solution, comment donc le complexe x ne doit pas vérifier simultanément ces 2 relations.

u(x)=0 => x=a+2i, a réel
v(x)=0 => x=1+ib, b réel
donc u(x)=v(x)=0 => x=a+2i=1+ib => x=1+2i.

Cela était le 1er point. Le 2ème point est que dans ton système de départ, il n'est précisé nulle part dans quel ensemble on cherche les solutions. En général pour une variable complexe, on utilise z, justement pour se réserver la possibilité de poser z=x+iy. D'utiliser x variable complexe est justement fait pour embrouiller.

[Razes]

Bonsoir tout le monde,
, où .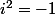

Je ne me pose pas de question, je résous dans car 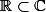: Avec:
Le terme de gauche de chacune des deux équations est réel et positif (car c'est un module), le terme de droite doit donc l'être aussi.

Le second terme de l'équation (1):
; Donc :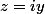
De plus, on doit avoir:


Donc avant de chercher et , il faut que le domaine de définition soit tel que:
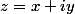et

Le second terme de l'équation (2):

De plus, on doit avoir:

Donc avant de chercher et , il faut que le domaine de définition vérifie cette 2ème condition:
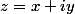et

Aucun domaine ne peut verifier les deux conitions, donc ça ne sert à rien d'aller plus loin. il n y a pas de solution dans donc non plus dans .