Système complexe.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
totololo
- Membre Naturel
- Messages: 81
- Enregistré le: 12 Juin 2010, 22:22
-
 par totololo » 02 Nov 2010, 10:35
par totololo » 02 Nov 2010, 10:35
Bonjour à toutes et à tous.
Petit problème quant à la résolution de ce système :
Trouver les couples (a,b) dans C² tels que :
| a²+b²=5+4i
| ab=-1
J'ai essayé de me servir du fait que a et b sont solutions de l'équation z²-(5+4i)z+1=0 .. mais je ne suis pas sur que ce soit vraiment correct, et je trouve des résultats faramineux et fort moches.
Merci de votre aide :happy2: .
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 02 Nov 2010, 10:51
par arnaud32 » 02 Nov 2010, 10:51
c'est une bonne idee en conservant la condition ab=-1
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 02 Nov 2010, 10:53
par Arnaud-29-31 » 02 Nov 2010, 10:53
totololo a écrit:a et b sont solutions de l'équation z²-(5+4i)z+1=0
Tu es sur de ça ? ... Attention ...
En effet il faut garder ab = -1.
-
totololo
- Membre Naturel
- Messages: 81
- Enregistré le: 12 Juin 2010, 22:22
-
 par totololo » 02 Nov 2010, 11:06
par totololo » 02 Nov 2010, 11:06
Mais comment garder cette condition?
Il faut : ab=-1 et (ab)²=1. Devrais-je résoudre 2 équations du seond degré?
-
totololo
- Membre Naturel
- Messages: 81
- Enregistré le: 12 Juin 2010, 22:22
-
 par totololo » 02 Nov 2010, 11:16
par totololo » 02 Nov 2010, 11:16
Quelqu'un peut - il me mettre sur une piste ?
Merci d'avance .
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 02 Nov 2010, 11:25
par arnaud32 » 02 Nov 2010, 11:25
tu resoud ton equation et ensute tu elimines les couples ne verifiant pas ab=-1 per ex.
-
totololo
- Membre Naturel
- Messages: 81
- Enregistré le: 12 Juin 2010, 22:22
-
 par totololo » 02 Nov 2010, 11:50
par totololo » 02 Nov 2010, 11:50
Donc il faut bien que je résolve l'équation z² - (5+4i)+1=0 ?
Je tombe sur des solutions très compliquées, ca m'étonnerait qu'il faille que je fasse ca.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 02 Nov 2010, 12:08
par arnaud32 » 02 Nov 2010, 12:08
a²+b²=s
ab=p
u=a²
v=b²
u, v sont solutions de (z-s/2)²-(s/2)²+p²=z²-sz+p²=0
c²=(s/2)²-p²
tu as u=s/2+c et v=s/2-c (ou le contraire)
et donc
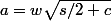
et
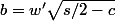
avec w et w' dans {-1,1}
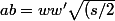^2-c^2})
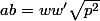
a toi de finir
-
totololo
- Membre Naturel
- Messages: 81
- Enregistré le: 12 Juin 2010, 22:22
-
 par totololo » 02 Nov 2010, 12:37
par totololo » 02 Nov 2010, 12:37
arnaud32 a écrit:a²+b²=s
ab=p
u=a²
v=b²
u, v sont solutions de (z-s/2)²-(s/2)²+p²=z²-sz+p²=0
c²=(s/2)²-p²
tu as u=s/2+c et v=s/2-c (ou le contraire)
et donc
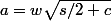
et
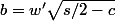
avec w et w' dans {-1,1}
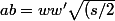^2-c^2})
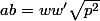
a toi de finir
Je n'ai pas compris : c²=(s/2)²-p² . Kezako?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 02 Nov 2010, 12:39
par arnaud32 » 02 Nov 2010, 12:39
une constante qui permet de simplifier tes calculs ...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
