Surjectivité

[Genrxtsey]

Bonjour, j'ai une question

voici l'exercice :
La fonction f(x)=x²-2x+1 est-elle surjective ?
elle est définie sur f: [1; +inf [ -> R

Réponse du prof :
f(x)= x²-2x+1=(x-1)²

f(x) n'est pas surjective car prenons y=-1
l'équation f(x)=-1 d'inconnue x appartient à [1; +inf [
n'a pas de solution dans [1; + inf [ car :
* -1<0
* pour tout x appartenant à R, (x-1)²>0

Oui mais pour y>0
il y a des solutions donc f(x) est surjective ??

[pokkk]

Un fonction f: A->B est surjective si chaque élément de B a un antécédent dans A. Dans ton cas il faudrait que tous les éléments de R puissent être exprimés sous la forme de (x-1)^2 avec x dans [1;+inf [.

Or (x-1)^2=-1 n'a pas de solution avec x dans [1;+inf [. Donc f n'est pas surjective.

Le fait que pour y>0 il y ait des solutions pour f(x)=y avec x dans [1; +inf [ signifie que si la fonction f avait été définie telle que f: [1; +inf [ -> [0;+inf [ elle aurait été surjective. Mais ce n'est pas le cas car elle a été définie de [1; +inf [ dans R.

[Genrxtsey]

Par exemple pour f(x)= - racine de ( x-4)

f(x)=y
ce qui donne
- racine(x-4) = y

On discute selon y :
y>0 n'admet aucune solution

mais la fonction est surjective car selon y<0
Racine (x-4) = -y
x=4+y² qui est la seule et l'unique soluti

[beagle]

Bonjour, j'ai une question

voici l'exercice :
La fonction f(x)=x²-2x+1 est-elle surjective ?
elle est définie sur f: [1; +inf [ -> R

Réponse du prof :
f(x)= x²-2x+1=(x-1)²

f(x) n'est pas surjective car prenons y=-1
l'équation f(x)=-1 d'inconnue x appartient à [1; +inf [
n'a pas de solution dans [1; + inf [ car :
* -10

Oui mais pour y>0
il y a des solutions donc f(x) est surjective ??

Comme le dit pokkk, l'important c'est l'ensemble de départ et l'ensemble d'arrivée,
si f arrive dans R, alors seuls des carrés donc des positifs vont recevoir une flèche = auont un ou deux atcd, donc il existe tout R- où les éléments n'auront pas d'antécédents, donc cela ne sera pas surjectif.
Le méli mélo que tu fais se complique d'un drole d'ensemble de définition, pourquoi choisit-on l'ensemble de départ [1; + inf [, c'est mystérieux, m'enfin...

[Ben314]

Si un jour on te demande "la fonction est elle injective ? surjective ? bijective ?"
Il n'y a qu'une seule réponse à donner : sans savoir ce qu'on prend comme ensemble de départ et d'arrivé, la question n'a pas de sens !

Par exemple,
- Elle n'a pas de sens si on prend comme ensemble de départ ou (quelque soit l'ensemble d'arrivé)
- Elle n'a pas de sens non plus si on prend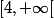 comme ensemble de départ et 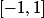comme ensemble d'arrivé (car par exemple 104 est dans l'ensemble de départ et son image n'est pas dans l'ensemble d'arrivé)
- Si on prend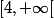 comme départ et comme arrivé, elle est bien définie, injective mais pas surjective.
- Si on prend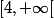 comme départ et 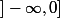comme arrivé, elle est bien définie, injective et surjective (donc bijective)...

Le cas a mémoriser c'est :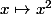
- De dans , elle n'est ni injective, ni surjective.
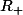- De dans , elle est injective, mais pas surjective.
- De dans 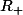, elle n'est pas injective, mais elle est surjective.
- De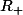 dans 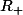, elle est injective et surjective.



En fait, les mots "injectifs", "surjectifs", "bijectifs" s'appliquent à des... applications et une application, c'est plus qu'une fonction : c'est une fonction f PLUS un ensemble de départ et un ensemble d'arrivé (et il faut évidement que f(x) soit calculable pour tout élément du départ ET que f(x) appartienne à l'ensemble d'arrivé)