Surjections avec SageMath
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Batiste
- Messages: 2
- Enregistré le: 10 Nov 2019, 21:00
-
 par Batiste » 10 Nov 2019, 21:12
par Batiste » 10 Nov 2019, 21:12
Bonsoir,
Après pas mal de boulot et de recherches, j'ai réussi à démontrer que le nombre d'applications surjectives d'un ensemble à n éléments vers un ensemble à n' éléments est :
S(n,n')
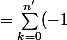^{k} \binom{n'}{k} (n'-k)^{n})
Malheureusement, et là est le problème, il faut le "tester avec SageMath", ayant une connaissance nulle dans ce logiciel, je cherche quelques âmes charitables qui pourraient éventuellement m'aider...
Merci d'avance et bonne soirée,
Batiste.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6133
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 10 Nov 2019, 23:31
par GaBuZoMeu » 10 Nov 2019, 23:31
Peut-être fabriquer l'ensemble des surjections de m dans n (à partir de FiniteSetMaps) et vérifier que le cardinal de cet ensemble est bien celui donné par la formule pour quelques valeurs de m et n ?
-
Batiste
- Messages: 2
- Enregistré le: 10 Nov 2019, 21:00
-
 par Batiste » 11 Nov 2019, 16:27
par Batiste » 11 Nov 2019, 16:27
J'ai fait quelques recherches sur cette commande FiniteSetMaps, est-ce que je dois fabriquer l'ensemble de toutes les cartes de {1, 2, ..., n} à {1, 2, ..., n'} ? Ou le fait de devoir fabriquer l'ensemble des surjections implique une autre précision dans la commande ?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6133
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 11 Nov 2019, 17:46
par GaBuZoMeu » 11 Nov 2019, 17:46
Maps, ça ne se traduit pas par cartes !!! Mais par applications.
Ce que je te suggère, en utilisant FiniteSetMaps :
faire une procédure qui prends en entrée les entiers m et n et retourne le nombre de surjections de m (ensemble à m éléments) dans n (ensemble à n éléments).
Pour ça, on initialise un compteur à 0 et on fait défiler les éléments f de FiniteSetMaps(m,n) en ajoutant 1 au compteur quand f est surjective, c.-à-d. quand l'ensemble image de f est de cardinal n.
Ça prend six petites lignes de code.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
