Bonjour,
Je souhaiterais connaître la surface du rectangle (en bleu) en fonction de sa largeur (L) et du diamètre/rayon du cercle. Schéma ci dessous.
https://imgur.com/a/kMUYzXB
Je voulais le calculer graçe à une intégrale mais je ne sais pas quelle fonction intégrer.
Merci d'avance.
PS : Comment est-ce que je peut insérer une image directement dans le texte?
Surface d'un rectangle contenu dans un cercle
7 messages
- Page 1 sur 1
Re: Surface d'un rectangle contenu dans un cercle
J'opterais pour calculer l'aire en blanc puis utiliser =\pi r^2-\mathcal{A}(\mathrm{blanc})) où
où  est le rayon du cercle. On va calculer l'aire de la partie blanche à droite, il faut déjà savoir quelle fonction intégrer. L'équation cartésienne d'un cercle de rayon
est le rayon du cercle. On va calculer l'aire de la partie blanche à droite, il faut déjà savoir quelle fonction intégrer. L'équation cartésienne d'un cercle de rayon  et disons ici centré en O est
et disons ici centré en O est 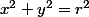 donc
donc  et donc la fonction
et donc la fonction =\sqrt{r^2-x^2}) dessine un demi-cercle de centre
dessine un demi-cercle de centre  et de rayon
et de rayon  . Il faut maintenant savoir sur quel domaine on intègre, si on résout l'équation
. Il faut maintenant savoir sur quel domaine on intègre, si on résout l'équation =\frac{L}{2}) on a gagné puisque si
on a gagné puisque si  désigne la solution positive de cette équation, on aura à intégrer sur
désigne la solution positive de cette équation, on aura à intégrer sur  . Donc
. Donc =\frac{L}{2}\iff r^2-x^2=\frac{L^2}{4}\iff x=\pm\sqrt{r^2-\frac{L^2}{4}}) donc
donc  . Finalement
. Finalement =2\int_{-\alpha}^{\alpha}f(x)dx=4\int_0^{\alpha}f(x)dx) car
car  est paire. Je te laisse finir (tu pourras faire un changement de variable et poser
est paire. Je te laisse finir (tu pourras faire un changement de variable et poser 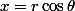 ).
).
Re: Surface d'un rectangle contenu dans un cercle
Pas besoin d'intégrale !
Ton "rectangle" n'est pas un rectangle, c'est plutôt une tranche de disque. Tu peux le décomposer en découpant selon les "diagonales" en deux triangles et deux secteurs angulaires
Si est la largeur de la tranche centrée et
est la largeur de la tranche centrée et  le rayon du disque, tu peux sans doute calculer en fonction de
le rayon du disque, tu peux sans doute calculer en fonction de  et
et  les dimensions des triangles et l'angle d'ouverture des secteurs circulaires. De là, il est facile d'obtenir l'aire de la tranche.
les dimensions des triangles et l'angle d'ouverture des secteurs circulaires. De là, il est facile d'obtenir l'aire de la tranche.
Ton "rectangle" n'est pas un rectangle, c'est plutôt une tranche de disque. Tu peux le décomposer en découpant selon les "diagonales" en deux triangles et deux secteurs angulaires
Si
Re: Surface d'un rectangle contenu dans un cercle
GaBuZoMeu a écrit:Pas besoin d'intégrale !
Ton "rectangle" n'est pas un rectangle, c'est plutôt une tranche de disque. Tu peux le décomposer en découpant selon les "diagonales" en deux triangles et deux secteurs angulaires
Siest la largeur de la tranche centrée et
le rayon du disque, tu peux sans doute calculer en fonction de
et
les dimensions des triangles et l'angle d'ouverture des secteurs circulaires. De là, il est facile d'obtenir l'aire de la tranche.
En effet, c'est aussi simple que ça.
Re: Surface d'un rectangle contenu dans un cercle
@tuvasbien
Merci pour ta réponse
Mais je ne comprends pas pourquoi on intégre pas de cette façon : Pour trouver la surface blanche.
Pour trouver la surface blanche.
Aussi je ne comprends ce que est censé représenter.
est censé représenter.
Merci pour ta réponse
Mais je ne comprends pas pourquoi on intégre pas de cette façon :
Aussi je ne comprends ce que
Re: Surface d'un rectangle contenu dans un cercle
Si tu traces le graphe de f, tu remarqueras que le x qui joue le rôle de variable d'intégration se situe sur la frontière verticale entre la zone bleue et la zone blanche. Le  est tel que la longueur de la frontière verticale entre la zone bleue et la zone blanche est
est tel que la longueur de la frontière verticale entre la zone bleue et la zone blanche est 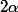 , il sert à savoir où se balade le x lorsqu'on intègre.
, il sert à savoir où se balade le x lorsqu'on intègre.
Re: Surface d'un rectangle contenu dans un cercle
@tuvasbien
La frontière verticale entre la zone bleue et la zone blanche est à x = L/2, non?
La frontière verticale entre la zone bleue et la zone blanche est à x = L/2, non?
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
