Surface d'un cône de révolution

[Anaisdeistres]

Bonjour,

Donnez une description analytique d’une surface conique obtenue par la révolution d’une droite génératrice autour d’un axe de révolution. Vous
pouvez choisir la droite génératrice que vous voulez.

Ok pour la formule de la surface d'un cône de révolution. Quelle est cette droite ? De la forme ax+b mais cela correspond à quoi dans la formule ?

(Pourquoi je suis en Maths ?)

[tournesol]

On rapporte l'espace à un repère orthonormé (O , i , j , k )
Le cone sera de sommet O et d'axe Oz .
La generatrice est la droite du plan xOz dont l'équation dans ce plan est z=ax avec a non nul .
M(x , y , z ) appartient au cône ssi M appartient au cercle de centre A(0 , 0 , z) , de rayon |z|/|a| , et d'axe Oz . Fais un dessin pour t'en convaincre .
Dans le plan horizontal qui passe par A , ce cercle a pour équation
l'équation du cône est donc et le demi angle au sommet est arctan(1/|a|)
En général cette equation est de la forme avec k réel strictement positif .
le demi angle au sommet est egal à arctan(1/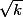
l'equation d'un cône de sommet O et d'axe Oy est alors de la forme
si l'axe est Ox l'equation est

[tournesol]

Erreur avant dernière ligne où est a remplacer par

[LB2]

Quelle est cette droite ? De la forme ax+b mais cela correspond à quoi dans la formule ?

2 remarques très importantes :

- "De la forme ax+b" ne veut rien dire et ne désigne pas une équation.

- Si tu veux dire que l'équation d'une droite affine est de la forme y=ax+b, c'est vrai dans le plan, mais faux dans l'espace. Car dans l'espace les points ont trois coordonnées, x, y, et z.

[Anaisdeistres]

Choisissez un plan d’intersection non-nulle avec la surface conique ci-haut, et donnez-en une description analytique.

Dans un espace affine muni d'un repère, on appelle conique tout ensemble de points M(x, y) vérifiant une égalité de la forme

Ax^{2}+2Bxy+Cy^{2}+2Dx+2Ey+F=0

où A, B, C, D, E, F sont des constantes telles que (A,B,C) ≠ (0,0,0).

Décrivez analytiquement la section conique ainsi obtenue c’est-à-dire, donnez l’équation cartésienne ainsi obtenue. Spécifiez le type de conique obtenue,
même si elle est dégénérés.

Ensuite j'étudie le cas ab différent de 0 et a supérieure à 0 et b supérieure à 0 et si k supérieur à 0 alors c'est une ellipse ... Et je fais tous les cas possible (étude que je vais trouver sur internet)

C'est cela ?