Sur le DL
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
theboss1er
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Sep 2008, 18:34
-
 par theboss1er » 13 Sep 2008, 19:16
par theboss1er » 13 Sep 2008, 19:16
bonjour
j'ai le droit de dire que exp( -ln(n) +o(ln(n)) ) = 1/n * o(1/n) ?
-
Satto
- Membre Naturel
- Messages: 32
- Enregistré le: 21 Sep 2007, 19:28
-
 par Satto » 13 Sep 2008, 19:46
par Satto » 13 Sep 2008, 19:46
theboss1er a écrit:bonjour
j'ai le droit de dire que exp( -ln(n) +o(ln(n)) ) = 1/n * o(1/n) ?
Je ne pense pas car a priori tu as dejas utilisé un DL pour arriver à se résultat il te faut trouver un dl de exp( -ln(n)). Pour information le dl que tu propose n'est pas un dl classique (il à un nom bien speciale) et il ne dérive pas de la formule de taylor. Est tu sur de t calcul réalisé juste avant?
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 13 Sep 2008, 19:53
par abcd22 » 13 Sep 2008, 19:53
Bonsoir,
theboss1er a écrit:j'ai le droit de dire que exp( -ln(n) +o(ln(n)) ) = 1/n * o(1/n) ?
Non car par exemple la suite constante égale à 1 est un o(ln n), et exp(- ln(n) + 1) = e/n.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 13 Sep 2008, 19:57
par leon1789 » 13 Sep 2008, 19:57
theboss1er a écrit:bonjour
j'ai le droit de dire que exp( -ln(n) +o(ln(n)) ) = 1/n * o(1/n) ?
o(ln(n)) est une "fonction" abstraite qui peut s'écrire ln(n).e(n) avec lim e(n)=0.
Que devient ton expression quand tu remplaces o(ln(n)) par ln(n).e(n) ?
-
theboss1er
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Sep 2008, 18:34
-
 par theboss1er » 13 Sep 2008, 19:59
par theboss1er » 13 Sep 2008, 19:59
j'ai voulu faire un DL de (1 - ln(n)/n )^n pour en trouver un équivalent
donc j'ai mis en Exp et j'ai fait un DL de ln(1-u) avec u=ln(n)/n
mais après j'ai l'exp d'un DL et je bloque...
-
Cauchy3
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Aoû 2008, 21:57
-
 par Cauchy3 » 13 Sep 2008, 20:00
par Cauchy3 » 13 Sep 2008, 20:00
theboss1er a écrit:bonjour
j'ai le droit de dire que exp( -ln(n) +o(ln(n)) ) = 1/n * o(1/n) ?
Non, par ce que
)})
n'est pas égal à o(

) il suffit de tourner à la définition de o(Un).
Cependant et si j'ai bien compris votre question on peux écrire en premier lieu :
+o(ln(n))}=e^{-ln(n)} e^{o(ln(n))}=\frac{1}{n} e^{o(ln(n)))
Est ce que tu cherches la suite?
satto a écrit:Pour information le dl que tu propose n'est pas un dl classique (il à un nom bien spéciale) et il ne dérive pas de la formule de Taylor.
DL suivant l'échelle
)
-
theboss1er
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Sep 2008, 18:34
-
 par theboss1er » 13 Sep 2008, 20:03
par theboss1er » 13 Sep 2008, 20:03
mon objectif étant de trouver un équivalent de la suite je ne vois pas trop...
en plus exp(o(ln(n))) ca fait bizarre

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 13 Sep 2008, 20:04
par leon1789 » 13 Sep 2008, 20:04
theboss1er a écrit:j'ai voulu faire un DL de (1 - ln(n)/n )^n pour en trouver un équivalent
donc j'ai mis en Exp et j'ai fait un DL de ln(1-u) avec u=ln(n)/n
mais après j'ai l'exp d'un DL et je bloque...
L'idée du DL est bonne.
Fais voir tes calculs stp.
-
theboss1er
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Sep 2008, 18:34
-
 par theboss1er » 13 Sep 2008, 20:08
par theboss1er » 13 Sep 2008, 20:08
alors :
u(n) = exp(n * ln (1-ln(n)/n))
et ln(1-ln(n)/n) = -ln(n)/n + o(ln(n)/n)
donc u(n) = exp( -ln(n) + o(ln(n)))
-
theboss1er
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Sep 2008, 18:34
-
 par theboss1er » 13 Sep 2008, 20:19
par theboss1er » 13 Sep 2008, 20:19
mon problème en fait vient à la fin du DL je pense
je ne trouve pas d'équivalent (ou plutot je ne sais pas comment faire ...)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 13 Sep 2008, 22:25
par leon1789 » 13 Sep 2008, 22:25
theboss1er a écrit:alors :
u(n) = exp(n * ln (1-ln(n)/n))
et ln(1-ln(n)/n) = -ln(n)/n + o(ln(n)/n)
donc u(n) = exp( -ln(n) + o(ln(n)/n))
Si tu bouffes toute l'info dans le o(..), ça ne va pas :id:
Maintenant, avec le
o(ln(n)/n), c'est bon ! Montre que u(n) = 1/n + o(1/n)
-
theboss1er
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Sep 2008, 18:34
-
 par theboss1er » 13 Sep 2008, 22:29
par theboss1er » 13 Sep 2008, 22:29
vu que je multiplie par n : n*o(ln(n)/n) = o(ln(n)) non ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 13 Sep 2008, 22:30
par leon1789 » 13 Sep 2008, 22:30
theboss1er a écrit:alors :
u(n) = exp(n * ln (1-ln(n)/n))
et ln(1-ln(n)/n) = -ln(n)/n + o(ln(n)/n)
donc u(n) = exp( -ln(n) + o(ln(n)))
Ok, ton DL de ln(1+x) n'est pas suffisant : fais le à un ordre un poil plus grand.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 13 Sep 2008, 22:30
par leon1789 » 13 Sep 2008, 22:30
theboss1er a écrit:vu que je multiplie par n : n*o(ln(n)/n) = o(ln(n)) non ?
oui, je me suis pris les pieds

, mais je viens de corriger...

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 13 Sep 2008, 22:35
par leon1789 » 13 Sep 2008, 22:35
avec ln(1+x) = x-x²/2+o(x²) et x=ln(n)/n, les choses s'arrangent et tu montres que u(n) = 1/n + o(1/n)
-
theboss1er
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Sep 2008, 18:34
-
 par theboss1er » 13 Sep 2008, 22:41
par theboss1er » 13 Sep 2008, 22:41
ok il me reste u(n) = 1/n * exp(-(ln(n))^2/n + o((ln(n))^2/n) ) et je ne vois pas comment poursuivvre :s
-
theboss1er
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Sep 2008, 18:34
-
 par theboss1er » 13 Sep 2008, 23:01
par theboss1er » 13 Sep 2008, 23:01
pourriez-vous me montrer votre démonstration s'il vous plaît ? je désespère :(
-
mathelot
 par mathelot » 14 Sep 2008, 08:00
par mathelot » 14 Sep 2008, 08:00
bjr,
La quantité dans l'exponentielle tend vers zéro.
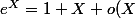)
}{n}+o(\frac{\ln^2(n)}{n}) \right))
les termes négligés ont

au dénominateur
}{n^2}+o(\frac{\ln^2(n)}{n^2}))
-
theboss1er
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Sep 2008, 18:34
-
 par theboss1er » 14 Sep 2008, 09:39
par theboss1er » 14 Sep 2008, 09:39
a ouii !!
désolé j'étais fatigué je cherchais à avoir du exp(1+u) avec u-->0
merci beaucoup tout le monde :king2:
a+ :zen:
-
theboss1er
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Sep 2008, 18:34
-
 par theboss1er » 14 Sep 2008, 10:26
par theboss1er » 14 Sep 2008, 10:26
donc en ayant ce DL je peux me ramener à u(n) = 1/n + o(1/n) ? pour dire que c'est équivalent ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
