Soit n un entier naturel non nul.
Une urne Un contient n boules numérotées de 1 à n. On effectue dans cette urne une succession de tirages dune boule, en appliquant la règle suivante : si une boule tirée porte le numéro k,avant de procéder au tirage suivant, on enlève de lurne toutes les boules dont le numéro est supérieur ou égal à k.
On note X , la variable aléatoire égale au nombre de tirages nécessaires pour vider lurne Un de toutes ses boules.
Quelqu'un pourrai m'expliquer comment trouver les lois de Xn et comment calculer leur espérance
Sujet ESC 1999
2 messages
- Page 1 sur 1
Si on note  , la variable aléatoire égale au nombre de tirages nécessaires pour vider lurne
, la variable aléatoire égale au nombre de tirages nécessaires pour vider lurne  alors,
alors,
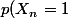=\frac{1}{n}) et, pour tout
et, pour tout  ,
, =\frac{1}{n}\sum_{j=1}^{n-1}P(X_j=k-1)\)
(la première boule tirée est la boule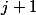 et il faut
et il faut 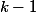 tirage pour vider l'urne qui ne contient plus que les boules 1 à
tirage pour vider l'urne qui ne contient plus que les boules 1 à  )
)
On en déduit que, pour , on a
, on a
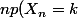- (n-1)p(X_{n-1}=k)=\sum_{j=1}^{n-1}P(X_j=k-1)-\sum_{j=1}^{n-2}P(X_j=k-1)=p(X_{n-1},k-1))
c'est à dire=\frac{n-1}{n} p(X_{n-1}=k)+\frac{1}{n}p(X_{n-1},k-1)\ (*))
Si on note le polynôme générateur de
le polynôme générateur de  , c'est à dire
, c'est à dire =\sum_{k\geq 0} p(X_n=k)T^k) alors on a
alors on a =T) et la formule
et la formule ) dit que
dit que 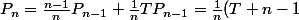P_{n-1}) et on en déduit (par récurrence) que
et on en déduit (par récurrence) que 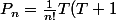(T+2)...(T+n-1))
Cela permet d'avoir assez simplement l'espérance de qui est
qui est =P_n'(1))
(la première boule tirée est la boule
On en déduit que, pour
c'est à dire
Si on note
Cela permet d'avoir assez simplement l'espérance de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
