Sujet de concours - formules de Frenet
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ze zoune
- Membre Relatif
- Messages: 166
- Enregistré le: 01 Mai 2008, 16:19
-
 par ze zoune » 24 Avr 2012, 14:20
par ze zoune » 24 Avr 2012, 14:20
Bonjour à tous,
J'ai quelques soucis dans la résolution d'un problème de concours, il s'agit de l'épreuve de Maths A de la banque PT 2005 (
énoncé).
La question I-2 nous demande de rappeler les formules de Frenet, ce que j'ai fait:

et

.
Il s'agit ensuite de montrer qu'il existe une fonction k (à déterminer) telle que:
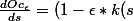)* \vec{\tau}(s))
,
où
 = c(t) + \epsilon*\vec{n}(t))
,

un réel et c une parabole de paramétrisation
=t \\<br />y(t)=t^2<br />\end{array}<br />\right.)
-------------
Le corrigé indique
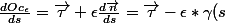*\vec{tau}=\vec{\tau}*(1 - \epsilon*\gamma (s)))
Pourriez-vous m'expliquer l'origine de la première égalité ?
Merci beaucoup !
-
geegee
- Membre Rationnel
- Messages: 799
- Enregistré le: 11 Mai 2008, 13:17
-
 par geegee » 24 Avr 2012, 14:43
par geegee » 24 Avr 2012, 14:43
ze zoune a écrit:Bonjour à tous,
J'ai quelques soucis dans la résolution d'un problème de concours, il s'agit de l'épreuve de Maths A de la banque PT 2005 (
énoncé).
La question I-2 nous demande de rappeler les formules de Frenet, ce que j'ai fait:

et

.
Il s'agit ensuite de montrer qu'il existe une fonction k (à déterminer) telle que:
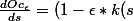)* \vec{\tau}(s))
,
où
 = c(t) + \epsilon*\vec{n}(t))
,

un réel et c une parabole de paramétrisation
=t \\<br />y(t)=t^2<br />\end{array}<br />\right.)
-------------
Le corrigé indique
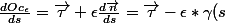*\vec{tau}=\vec{\tau}*(1 - \epsilon*\gamma (s)))
Pourriez-vous m'expliquer l'origine de la première égalité ?
Merci beaucoup !
Bonjour,
 = c(t) + \epsilon*\vec{n}(t))
/ds = dc(t)/ds + \epsilon*d\vec{n}(t)/ds)
comme c une parabole de paramétrisation
=t <br />y(t)=t^2<br />\end{array}<br />\right.)
alors d Oc(t)/ds=
)
,
[TEX]\left\{
\begin{array}
dx(t)/dt=1 \\
dy(t)/dt=t*2
\end{array}
en dérivant c et en utilisant les formules on a le résultat
-
ze zoune
- Membre Relatif
- Messages: 166
- Enregistré le: 01 Mai 2008, 16:19
-
 par ze zoune » 24 Avr 2012, 14:59
par ze zoune » 24 Avr 2012, 14:59
J'ai compris, merci beaucoup !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
