Sujet concour ingé territorial

[Vlad-Drac]

Bonjour je m'entraine sur un sujet et je n'arriv pas au bout pourriez vous maider SVP ?

soit f l'endomorphisme representé par
A=
1 2 2
-1 1 -1
1 0 2

Question I

1-a) Soit le vecteur u (0,1,-1). Calculer les coordonnées de f (u). Les calculs seront

détaillés

1-b) Que peut-on en déduire pour u et le réel 2 ?

jai trouvé f(u)=2*u on en debuit que u est un vecteur propre associé à la valeur propre 2

Question 2 : (2,5 points)

Si elles existent, on note et les valeurs propres réelles de f rangées par ordre croissant.

2-a) Calculer les valeurs propres de f en détaillant les calculs.

jai trouvé 2 de multiplicité 1 et 1 de multiplicité 2

2-b) Soit E1, le sous-espace propre associé à la valeur propre 1 . Montrer que E1 est de dimension 1
il est engendré par le vecteur (1,1,-1)
2-c) Donner un vecteur propre associé à la valeur propre 1.
on a f(1,1,-1)=1*(1,1,-1)
donc cest un vecteur propre.

2-d) Expliquer pourquoi A n'est pas diagonalisable.
car E1 n'est pas de dimension 2...


Question 3 : (1,75 points) Soit le vecteur v= (1, 1,-1)

3-a) Vérifier et justifier que (u, v, e1) forme une base de On notera B' cette nouvelle base.
fait

3-b) Calculer les coordonnées de f (u) et f (v) dans La base B'.
f(u)=(0,2,0)
f(v)=(1,1,-1)


3-c) En déduire qu'il existe une matrice inversible M et une matrice triangulaire supérieure T telles que

A= M -l * T * M.

On explicitera M et T.

je pensais que M etait formé des vecteur propres placé en colonne comme ceci
0 1 0
1 1 0
-1 -1 1
et T=
2 0 a
0 1 b
0 0 1

mais en utilisant la formule A=M-1 * T * M pour retrouver a et b ca ne marche pas.

quelqun pourrait il maider ?

[Ben314]

Salut,
Tout le début (jusqu'au 3)), mais après, c'est pas clair...
Déjà, si u=(0,1,-1) ; v=(1,1,-1) et e1=(1,0,0) alors (u,v,e1) n'est pas une base.

Ensuite, où que soit ton erreur de "recopiage" concernant la susdite base, vu que f(u)=2u=2.u+0.v+0.e1 les coordonnées de u dans la base (u,v,e1) sont (2,0,0).
De même, vu que f(v)=v=0.u+1.v+0.e1, les coordonnées de v dans la base (u,v,e1) sont (0,1,0)

[Ben314]

Salut,
Tout le début (jusqu'au 3)), mais après, c'est pas clair...
Déjà, si u=(0,1,-1) ; v=(1,1,-1) et e1=(1,0,0) alors (u,v,e1) n'est pas une base.

Ensuite, où que soit ton erreur de "recopiage" concernant la susdite base, vu que f(u)=2u=2.u+0.v+0.e1 les coordonnées de u dans la base (u,v,e1) sont (2,0,0).
De même, vu que f(v)=v=0.u+1.v+0.e1, les coordonnées de v dans la base (u,v,e1) sont (0,1,0)

[Ben314]

Vu ce que tu écrit là :

je pensais que M etait formé des vecteur propres placé en colonne comme ceci
0 1 0
1 1 0
-1 -1 1

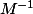avec comme 3em colonne (0,0,1) je suppute que le 3em vecteur de ta base, c'est w=(0,0,1) (qu'on appelle en général plutôt e3 que e1...)
Dans ce cas, cette matrice est effectivement la matrice dite "de passage de la base canonique B à la base B'=(u,v,w)" (sauf que c'est pas elle la matrice M de la fin : voir en bas...)
Et la matrice T dont te parle l'énoncé, c'est ce qu'on appelle "matrice de f dans la base B' " (la matrice donné au départ par l'énoncé étant "la matrice de f dans la base canonique f".
La matrice T s'obtient en mettant en colonne les coordonnées respectives de u,v,w dans la base B'=(u,v,w) donc effectivement la première colonne est (2,0,0) vu que f(u)=2u et la deuxième est (0,1,0) vu que f(v)=2v.
La troisième est (a,b,c) qui sont les coordonnées de f(w) dans B', c'est à dire les réels tels que f(w)=a.u+b.v+c.w et, effectivement, comme T est triangulaire, les valeur propres de f doivent apparaitre sur la diagonale et ça te dit (sans calculs) que c=1.

Sauf que :
1) Perso, pour calculer a et b, je résoudrait plutôt f(w)-w=a.u+b.v plutôt que de faire le produit matriciel.
2) Dans la "formule" , la matrice de passage de B à B' (celle qu'il y a dans la citation ci dessus), c'est pas , c'est ...

[Vlad-Drac]

tu as bien suputé ! pardon pour l'erreur de recopiage et merci pour tes indication je vais ressayer

[Vlad-Drac]

Super ça marche merci bcp !