Sujet agreg 2005
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ludo56
- Membre Relatif
- Messages: 338
- Enregistré le: 16 Juil 2007, 11:49
-
par ludo56 » 17 Jan 2010, 17:37
Bonjour!
Je bloque sur une question:
Soit
l'espace vectoriel complexe des familles
_{(m,n) \in \mathbb Z^2})
de nombres complexe.
Pour
_{(m,n) \in \mathbb Z^2} \in A)
, on pose :
\in \mathbb Z^2} |a_{m,n}|)
et
\in \mathbb Z^2} |a_{m,n}|^2)^{1/2})
.
On pose
= {
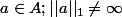
} et
= {
}.
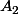
On pose également
un nombre complexe de module
.
Enfin, pour
 \in \mathbb Z^2)
on considere la famille
}a_{p,q}.b_{m-p,n-q})_{(p,q) \in \mathbb Z^2} = d_{p,q})
avec
et
deux éléments de
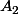
. On pose
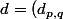_{(p,q) \in \mathbb Z^2})
.
Je dois montrer que
.
Je ne vois pas comment faire. J'ai pourtant une indication qui me dit d'utiliser l'inégalité de Cauchy-Schwarz mais je ne vois pas du tout comment l'appliquer.
Merci pour toutes réponses!
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
par Finrod » 17 Jan 2010, 18:09
Ben tu appliques directement, la somme des produit des modules, au carré est plus petite que le produit des sommes des modules au carré.
Peut être une des choses sivantes te gêne :
Cauchy scwartz s'applique aussi bien pour des intégrales que pour des sommes (qui sont des intégrales par rapport à des mesures discrètes).
Le
est de module 1 et donc disparait.
-
ludo56
- Membre Relatif
- Messages: 338
- Enregistré le: 16 Juil 2007, 11:49
-
par ludo56 » 18 Jan 2010, 10:35
merci beaucoup à vous deux! en fait je connaissais ce lien mais la correction du sujet de 2005 nous envoie sur le site dynamath qui ne marche plus depuis quelques semaines... quelqu'un est-il au courant? C'est vraiment dommage car il y a pas mal de choses intéressantes sur ce site.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
par Joker62 » 18 Jan 2010, 11:36
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
par Joker62 » 18 Jan 2010, 11:37
http://dynamaths.free.fr/L'auteur a déplacé autre part.
Certainement que l'autre serveur était KO.
-
vysy
- Membre Naturel
- Messages: 99
- Enregistré le: 18 Jan 2010, 10:43
-
par vysy » 18 Jan 2010, 11:59
ah moi aussi j'avais le même soucis merci!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
