Suites de syracuse
45 messages
- Page 2 sur 3 - 1, 2, 3
"Il y a des problèmes relatifs à cette suite. Par exemple:
La suite de Syracuse, pour ce qu'on en sait, renvoie toujours n'importe quel nombre n à 1 dans une seule boucle de longueur 3 (1,4,2,1,...). Dans cette hypothèse, montrer que pour les suites de forme 3n+a (au lieu de 3n+1), a entier naturel, il existe une infinité de valeurs pour a tel qu'on aboutit aussi à une seule boucle de longueur 3.
Rappel de l'algorithme de Syracuse: Si n pair---->n/2, si n impair---->3n+1, et on recommence avec le résultat."
Je me suis permis de remonter la question. Il s'agit bien d'une démonstration qui est demandée, pas d'informatique là dedans. Evidemment le a est impair, pour la division par 2. Je précise que si la suite de Syracuse 3n+1 a d'autres boucles que 1,4,2, alors ces suites 3n+a auront aussi d'autres boucles que 1,4,2. Et de même longueur que la 3n+1. Sinon, le temps de vol et l'altitude de ces suites 3n+a sont intimiment dépendants de la suite 3n+1.
C'est simple à expliquer et la recherche de telles suites n'est pas très longue.
La suite de Syracuse, pour ce qu'on en sait, renvoie toujours n'importe quel nombre n à 1 dans une seule boucle de longueur 3 (1,4,2,1,...). Dans cette hypothèse, montrer que pour les suites de forme 3n+a (au lieu de 3n+1), a entier naturel, il existe une infinité de valeurs pour a tel qu'on aboutit aussi à une seule boucle de longueur 3.
Rappel de l'algorithme de Syracuse: Si n pair---->n/2, si n impair---->3n+1, et on recommence avec le résultat."
Je me suis permis de remonter la question. Il s'agit bien d'une démonstration qui est demandée, pas d'informatique là dedans. Evidemment le a est impair, pour la division par 2. Je précise que si la suite de Syracuse 3n+1 a d'autres boucles que 1,4,2, alors ces suites 3n+a auront aussi d'autres boucles que 1,4,2. Et de même longueur que la 3n+1. Sinon, le temps de vol et l'altitude de ces suites 3n+a sont intimiment dépendants de la suite 3n+1.
C'est simple à expliquer et la recherche de telles suites n'est pas très longue.
déjà, avec u->3u+3 si n'est impair tu obtiens, SGDG le cycle 12,6,3 donc tu n'atteindra jamais 1! de plus cette boucle n'est évidemment jamais dans la vrai suite de Syracuse, sauf si tu initialise avec u=6*h*2^k, 6 et 12 n'apparaissent jamais( facile à voir en binaire) et si tu fais u->3u+2p+1, ta boucle terminale sera souvent variable et on n'atterri rarement!!
Exemple avec u->3U+7 et une initialisation avec u=201; boucle: 22, 11,40,20,10,5 et 42 termes calculés!
pour la même en partant de 2015 on arrive à la même et 64 termes calculés
pour la même en partant de 4179 on arrive à 28, 14 7 et 25 termes calculés.
Conclusion: je vais à Nice la semaine prochaine; je vais dire à ma meuf de ne pas s'affoler si je demande au commandant se bord s'il connait la vraie suite de Syracuse, celle qui atterrit toujours! :ptdr:
Exemple avec u->3U+7 et une initialisation avec u=201; boucle: 22, 11,40,20,10,5 et 42 termes calculés!
pour la même en partant de 2015 on arrive à la même et 64 termes calculés
pour la même en partant de 4179 on arrive à 28, 14 7 et 25 termes calculés.
Conclusion: je vais à Nice la semaine prochaine; je vais dire à ma meuf de ne pas s'affoler si je demande au commandant se bord s'il connait la vraie suite de Syracuse, celle qui atterrit toujours! :ptdr:
nodjim a écrit:@Paquito: Je ne pense pas avoir demandé que les suites retombent à 1: Seulement qu'elles tombent dans une boucle de longueur 3.
C'était seulement pour placer ma blague à 10 centimes d'!
Expérimentalement on trouve toujours une boucle, mais elle est ni unique, ni forcément de longueur 3( voir le contre exemple avec 3x+7) de plus tu peux arriver à 1 (toujours avec 3x=7) si tu par de u=3579 tu auras comme séquence: 64,32,16,8,4,2,1,10,5,22,11,40,20,10,5,22,
donc tu passes par 1 mais tu ne prends pas de carburant!
Mais ton problème est très intéressant.Et de plus pour 3x+3 ça a l'air de bien marcher.
Bon, alors je m'y colle...
On fixe k.
Partant de la suite "usuelle"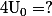 ;
;  , si on pose
, si on pose 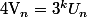 on obtient immédiatement
on obtient immédiatement ) ce qui permet d'associer "canoniquement" à une suite "usuelle" une suite vérifiant
ce qui permet d'associer "canoniquement" à une suite "usuelle" une suite vérifiant ) qui aura clairement les même propriétés concernant les (éventuels) cycles et/ou le fait d'être bornée et/ou... d'autres trucs...
qui aura clairement les même propriétés concernant les (éventuels) cycles et/ou le fait d'être bornée et/ou... d'autres trucs...
Dans l'autre sens, il y a une mini astuce vu que, si on part d'une suite vérifiant) mais telle que
mais telle que 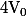 n'est pas multiple de
n'est pas multiple de 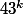 , on a l'impression (fausse... :zen:) qu'on ne peut pas "revenir en arrière" pour trouver une suite "usuelle" lui correspondant.
, on a l'impression (fausse... :zen:) qu'on ne peut pas "revenir en arrière" pour trouver une suite "usuelle" lui correspondant.
Sauf que, dans la deuxième formule de la relation) , on voit que, si la valuation 3-adique de
, on voit que, si la valuation 3-adique de 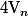 est
est 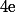 (i.e. si
(i.e. si 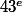 divise
divise 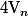 mais que
mais que 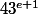 ne divise pas
ne divise pas 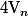 ) avec
) avec 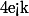 alors la valuation 3-adique de
alors la valuation 3-adique de 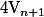 sera
sera 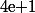 donc au bout d'un certain nombre d'itération de
donc au bout d'un certain nombre d'itération de ) on finira par tomber sur un
on finira par tomber sur un 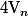 multiple de
multiple de 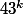 (vu qu'il est évidement exclu qu'on applique qu'un nombre fini de fois la deuxième formule de
(vu qu'il est évidement exclu qu'on applique qu'un nombre fini de fois la deuxième formule de ) ).
).
Et, à partir de ce terme là, la suite) sera issue d'une suite "usuelle"
sera issue d'une suite "usuelle" ) par la relation
par la relation 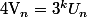 et elle héritera des propriétés de cette suite concernant l'existence d'un éventuel cycle, etc...
et elle héritera des propriétés de cette suite concernant l'existence d'un éventuel cycle, etc...
On fixe k.
Partant de la suite "usuelle"
Dans l'autre sens, il y a une mini astuce vu que, si on part d'une suite vérifiant
Sauf que, dans la deuxième formule de la relation
Et, à partir de ce terme là, la suite
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bon, alors je m'y colle...
On fixe k.
Partant de la suite "usuelle"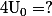 ;
;  , si on pose
, si on pose 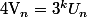 on obtient immédiatement
on obtient immédiatement ) ce qui permet d'associer "canoniquement" à une suite "usuelle" une suite vérifiant
ce qui permet d'associer "canoniquement" à une suite "usuelle" une suite vérifiant ) qui aura clairement les même propriétés concernant les (éventuels) cycles et/ou le fait d'être bornée et/ou... d'autres trucs...
qui aura clairement les même propriétés concernant les (éventuels) cycles et/ou le fait d'être bornée et/ou... d'autres trucs...
Dans l'autre sens, il y a une mini astuce vu que, si on part d'une suite vérifiant) mais telle que
mais telle que 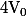 n'est pas multiple de
n'est pas multiple de 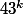 , on a l'impression (fausse... :zen:) qu'on ne peut pas "revenir en arrière" pour trouver une suite "usuelle" lui correspondant.
, on a l'impression (fausse... :zen:) qu'on ne peut pas "revenir en arrière" pour trouver une suite "usuelle" lui correspondant.
Sauf que, dans la deuxième formule de la relation) , on voit que, si la valuation 3-adique de
, on voit que, si la valuation 3-adique de 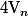 est
est 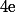 (i.e. si
(i.e. si 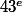 divise
divise 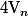 mais que
mais que 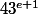 ne divise pas
ne divise pas 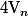 ) avec
) avec 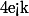 alors la valuation 3-adique de
alors la valuation 3-adique de 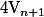 sera
sera 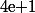 donc au bout d'un certain nombre d'itération de
donc au bout d'un certain nombre d'itération de ) on finira par tomber sur un
on finira par tomber sur un 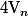 multiple de
multiple de 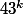 (vu qu'il est évidement exclu qu'on applique qu'un nombre fini de fois la deuxième formule de
(vu qu'il est évidement exclu qu'on applique qu'un nombre fini de fois la deuxième formule de ) ).
).
Et, à partir de ce terme là, la suite) sera issue d'une suite "usuelle"
sera issue d'une suite "usuelle" ) par la relation
par la relation 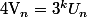 et elle héritera des propriétés de cette suite concernant l'existence d'un éventuel cycle, etc...
et elle héritera des propriétés de cette suite concernant l'existence d'un éventuel cycle, etc...
Bilan : On a une "presque bijection" entre les suites "usuelles" et celles vérifiant) , cette "presque bijection" étant suffisante en ce qui concerne l'étude de ce qui se passe pour n tendant vers l'infini (cycles ? bornée ?, etc...)
, cette "presque bijection" étant suffisante en ce qui concerne l'étude de ce qui se passe pour n tendant vers l'infini (cycles ? bornée ?, etc...)
On fixe k.
Partant de la suite "usuelle"
Dans l'autre sens, il y a une mini astuce vu que, si on part d'une suite vérifiant
Sauf que, dans la deuxième formule de la relation
Et, à partir de ce terme là, la suite
Bilan : On a une "presque bijection" entre les suites "usuelles" et celles vérifiant
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
C'est bon, je suis (con)vaincu!
Tu est quand même un phénomène Ben! Moi je m'étais arrêté à la période d'observation et à prouver que le cycle apparaissant ne contenait 1 que dans la suite de Syracuse.
Toute peine méritant salaire, une blagounette:
Quelle est la différence entre un pédophile et un surdoué?
Tu est quand même un phénomène Ben! Moi je m'étais arrêté à la période d'observation et à prouver que le cycle apparaissant ne contenait 1 que dans la suite de Syracuse.
Toute peine méritant salaire, une blagounette:
Quelle est la différence entre un pédophile et un surdoué?
Bonjour à tous,
Permettez moi de mettre mon grain de sel dans cette histoire de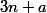 . Je vais plutôt considérer les suites compressées
. Je vais plutôt considérer les suites compressées 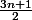 et
et 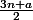 à la place, c'est plus simple et c'est aussi une question d'habitude :lol3: . Donc au lieu d'avoir un cycle trivial de longueur 3 (4,2,1,4,2,1,...) nous n'aurons plus qu'un cycle trivial de longueur de longueur 2 (2,1,2,1,...).
à la place, c'est plus simple et c'est aussi une question d'habitude :lol3: . Donc au lieu d'avoir un cycle trivial de longueur 3 (4,2,1,4,2,1,...) nous n'aurons plus qu'un cycle trivial de longueur de longueur 2 (2,1,2,1,...).
Considérons la suite
 = \left \{<br />\begin{array}[c c]<br />\frac{1}{2}(3n+a) & \quad \textit{si} \quad n \quad \textit{est impair} \\<br />\frac{1}{2} n & \quad \textit{si} \quad n \quad \textit{est pair} \\<br />\end{array}<br />\right .)
( doit être impair pour que
doit être impair pour que 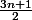 soit à nouveau entier).
soit à nouveau entier).
Il me semble que l'on peut voir:
 \forall a \geq 1) ,
,  impair, il existe un cycle trivial de longueur 2 qui est:
impair, il existe un cycle trivial de longueur 2 qui est: 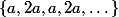
 \quad \textit{Si} \; a \equiv 0 \quad \pmod{2^k-3^{s}}) alors il existe un cycle de type
alors il existe un cycle de type ) (signifie un cycle de longueur
(signifie un cycle de longueur  contenant exactement
contenant exactement  impairs). De plus, il n'est pas unique (sauf si
impairs). De plus, il n'est pas unique (sauf si 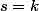 ou
ou 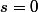 ).
).
Par exemple, prenons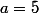 . On peut observer que
. On peut observer que 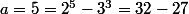 . On peut trouver les cycles:
. On peut trouver les cycles:
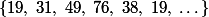
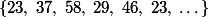
Si on prends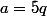 ,
,  entier, on pourra toujours avoir les cycles:
entier, on pourra toujours avoir les cycles:
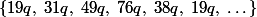
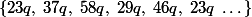
mais il est possible que d'autres s'y ajoute (dépendra de et notamment de ses diviseurs).
et notamment de ses diviseurs).
Par contre la réciproque n'est pas vraie me semble t'il (j'avais trouvé un contre-exemple, je peux vous le retrouver si cela vous intéresse), c'est à dire qu'on peut trouver un cycle de type) pour
pour 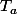 sans que l'on ait
sans que l'on ait 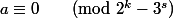 .
.
Cependant, si la conjecture est vraie, cad qu'il n'existe pas de cycles non triviaux dans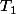 (la suite usuelle avec a=1), dans ce cas là on devrait avoir:
(la suite usuelle avec a=1), dans ce cas là on devrait avoir:
 \; \textit{dans} \; T_a \quad \Longrightarrow \quad \gcd(a,2^k-3^s) > 1) .
.
Pour prendre l'exemple cité plus haut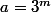 ,
,  entier: comme
entier: comme  =1) , si je ne me suis pas trompé il ne devrait normalement n'y avoir aucun cycle autre que
, si je ne me suis pas trompé il ne devrait normalement n'y avoir aucun cycle autre que 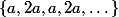 , donc aucun cycle non trivial. Mais cela serait une conséquence de la conjecture de syracuse.
, donc aucun cycle non trivial. Mais cela serait une conséquence de la conjecture de syracuse.
Donc démontrer la conjecture de Syracuse (la non-existence de cycles non triviaux) reviendrait à démontrer une réciproque partielle de 2), mais je ne sais pas si cela apporte vraiment quelquechose.
Voilà j'éspère que c'est pas trop du charabia ce que j'ai écrit. Il y a beaucoup de "il me semble" car j'avais noté ça une fois, mais je n'ai plus mes notes sur moi. Cependant ce n'était pas vraiment sorcier à trouver dans mon souvenir, donc si ça intéresse quelqu'un je peux vous le réecrire un peu plus tard. Mais bon j'imagine que vous n'aurez pas de mal à vérifier ça par vous même :happy3:
Bonne journée à vous
Permettez moi de mettre mon grain de sel dans cette histoire de
Considérons la suite
(
Il me semble que l'on peut voir:
Par exemple, prenons
Si on prends
mais il est possible que d'autres s'y ajoute (dépendra de
Par contre la réciproque n'est pas vraie me semble t'il (j'avais trouvé un contre-exemple, je peux vous le retrouver si cela vous intéresse), c'est à dire qu'on peut trouver un cycle de type
Cependant, si la conjecture est vraie, cad qu'il n'existe pas de cycles non triviaux dans
Pour prendre l'exemple cité plus haut
Donc démontrer la conjecture de Syracuse (la non-existence de cycles non triviaux) reviendrait à démontrer une réciproque partielle de 2), mais je ne sais pas si cela apporte vraiment quelquechose.
Voilà j'éspère que c'est pas trop du charabia ce que j'ai écrit. Il y a beaucoup de "il me semble" car j'avais noté ça une fois, mais je n'ai plus mes notes sur moi. Cependant ce n'était pas vraiment sorcier à trouver dans mon souvenir, donc si ça intéresse quelqu'un je peux vous le réecrire un peu plus tard. Mais bon j'imagine que vous n'aurez pas de mal à vérifier ça par vous même :happy3:
Bonne journée à vous
Oui, tu as forcément un cycle de longueur 2 (ou 3 selon la façon dont on compte), mais la question était "pour quelles valeurs de a la suite avec +a à la place de +1 a-t-elle qu'un unique cycle ?" (en supposant que c'est vrai pour a=1).ghostrider216 a écrit:C'est même vrai quelque soit a impair, on a le cycle {a,4a,2a,a,4a, etc}...
Et, comme tu le fait remarquer dans ton post. précédent, c'est faux pour beaucoup d'entiers (impairs) a : il y a effectivement toujours un cycle de longueur 2, ais très fréquemment, il y en a d'autres.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Oui, tu as forcément un cycle de longueur 2 (ou 3 selon la façon dont on compte), mais la question était "pour quelles valeurs de a la suite avec +a à la place de +1 a-t-elle qu'un unique cycle ?" (en supposant que c'est vrai pour a=1).
Et, comme tu le fait remarquer dans ton post. précédent, c'est faux pour beaucoup d'entiers (impairs) a : il y a effectivement toujours un cycle de longueur 2, ais très fréquemment, il y en a d'autres.
A priori si l'on prend
non?
Et ce n'est pas nécessaire de supposer que c'est vrai a=1
Si, tout à fait, sauf... que c'était pas ça la question de nodjim : il demandait à ce qu'il y ait un unique cycle de longueur 2 (ou 3 avec sa façon de compter)
sinon, concernant le "contre exemple" de ton post précédent, c'est lié au fait que, si 2^k-3s n'est pas premier ça risque de déconner.
Par exemple, avec k=6 et s=2 tu as 2^k-3^s=55 non premier, et effectivement en prenant a=11 (qui divise 2^k-3^s, mais qui n'est pas congru à 0 modulo 2^k-3^s) il y a un (k,s) cycle :
1 -> 7 -> 16 -> 8 -> 4 -> 2 (-> 1)
sinon, concernant le "contre exemple" de ton post précédent, c'est lié au fait que, si 2^k-3s n'est pas premier ça risque de déconner.
Par exemple, avec k=6 et s=2 tu as 2^k-3^s=55 non premier, et effectivement en prenant a=11 (qui divise 2^k-3^s, mais qui n'est pas congru à 0 modulo 2^k-3^s) il y a un (k,s) cycle :
1 -> 7 -> 16 -> 8 -> 4 -> 2 (-> 1)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Si, tout à fait, sauf... que c'était pas ça la question de nodjim : il demandait à ce qu'il y ait un unique cycle de longueur 2 (ou 3 avec sa façon de compter)
sinon, concernant le "contre exemple" de ton post précédent, c'est lié au fait que, si 2^k-3s n'est pas premier ça risque de déconner.
Par exemple, avec k=6 et s=2 tu as 2^k-3^s=55 non premier, et effectivement en prenant a=11 (qui divise 2^k-3^s, mais qui n'est pas congru à 0 modulo 2^k-3^s) il y a un (k,s) cycle :
1 -> 7 -> 16 -> 8 -> 4 -> 2 (-> 1)
Ah d'accord, alors je n'ai pas dû comprendre sa question alors. Quel serait un contre-exemple d'une valeur positive de a telle qu'on ait plusieurs cycles distincts de longueur 2?
Ce n'est pas
Mais bon c'est juste une reformulation de syracuse qui ne simplifie pas vraiment le problème.
J'ai mal formulé ma phrase : ce que voulais nodgim, ce n'est pas "un unique {cycle de longueur 2}", c'est à dire un seul cycle de longueur 2 plus éventuellement des tas d'autres de longueur autre que 2
Mais "{un unique cycle} de longueur 2", c'est à dire qu'en tout et pour tout, il y ait un seul cycle (de longueur quelconque) et qu'en plus cet unique cycle soit de longueur 2.
Avec a impair quelconque, on aura effectivement "un unique {cycle de longueur 2}" mais en général pas "{un unique cycle} de longueur 2" (i.e. il y aura d'autre cycles de longueur autres que 2)
Par contre, avec a=3^k alors on aura bien "{un unique cycle} de longueur 2" (si la conjecture est vrai).
Je sais pas si c'est clair cette fois...
Sinon, concernant le "Ce n'est pas qui doit diviser
qui doit diviser 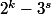 mais le contraire", moi il me semble bien que dans le cas que je mentionne, c'est bien a=11 qui divise 2^k-3^s=55 et pas le contraire... :ptdr:
mais le contraire", moi il me semble bien que dans le cas que je mentionne, c'est bien a=11 qui divise 2^k-3^s=55 et pas le contraire... :ptdr:
Mais "{un unique cycle} de longueur 2", c'est à dire qu'en tout et pour tout, il y ait un seul cycle (de longueur quelconque) et qu'en plus cet unique cycle soit de longueur 2.
Avec a impair quelconque, on aura effectivement "un unique {cycle de longueur 2}" mais en général pas "{un unique cycle} de longueur 2" (i.e. il y aura d'autre cycles de longueur autres que 2)
Par contre, avec a=3^k alors on aura bien "{un unique cycle} de longueur 2" (si la conjecture est vrai).
Je sais pas si c'est clair cette fois...
Sinon, concernant le "Ce n'est pas
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:J'ai mal formulé ma phrase : ce que voulais nodgim, ce n'est pas "un unique {cycle de longueur 2}", c'est à dire un seul cycle de longueur 2 plus éventuellement des tas d'autres de longueur autre que 2
Mais "{un unique cycle} de longueur 2", c'est à dire qu'en tout et pour tout, il y ait un seul cycle (de longueur quelconque) et qu'en plus cet unique cycle soit de longueur 2.
Avec a impair quelconque, on aura effectivement "un unique {cycle de longueur 2}" mais en général pas "{un unique cycle} de longueur 2" (i.e. il y aura d'autre cycles de longueur autres que 2)
Par contre, avec a=3^k alors on aura bien "{un unique cycle} de longueur 2" (si la conjecture est vrai).
Je sais pas si c'est clair cette fois...
Sinon, concernant le "Ce n'est pasqui doit diviser
mais le contraire", moi il me semble bien que dans le cas que je mentionne, c'est bien a=11 qui divise 2^k-3^s=55 et pas le contraire... :ptdr:
Ah d'accord je vois ce que voulais dire nodgim, dans ce cas là tu as évidemment raison!
oui dans ton exemple c'est bien a=11 qui divise 2^k-3^s=55, mais dans le point 2) de mon message c'était:
c'était tout ce que je voulais dire, mais je pense que c'était clair pour toi
45 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
