Suites: questions diverses
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Anonyme
 par Anonyme » 15 Oct 2005, 20:53
par Anonyme » 15 Oct 2005, 20:53
Bonsoir, j'ai plusieurs questions à vous poser.
1°) Pourquoi
}{\frac{1}{n^{\alpha}}} = 1)
, alors que
}{1+n} = 0)
?
2°) Pourquoi
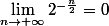
?
3°) Je dois étudier la nature des deux suites
_{n \in \mathbb{I}})
suivantes.
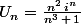
pour
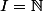
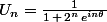
pour
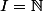
Comment s'y prendre?
Merci d'avance, et bonne soirée à tous.
-
jawad
- Membre Naturel
- Messages: 58
- Enregistré le: 11 Oct 2005, 22:41
-
 par jawad » 15 Oct 2005, 21:43
par jawad » 15 Oct 2005, 21:43
si lim q A tend vers +oo de ln f(A) = -oo alors lim q A tend vers +oo de f(A)=0
ç peut t'aider pour comprendre la 2eme question
-
Anonyme
 par Anonyme » 15 Oct 2005, 22:25
par Anonyme » 15 Oct 2005, 22:25
Euh...oui...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 15 Oct 2005, 22:51
par Nightmare » 15 Oct 2005, 22:51
Bonjour
Pour la premiere :
En posant

On est amené à chercher la limite de :
}{X})
lorsque X tend vers 0
On reconnait un nombre dérivée en 0, cette limite vaut donc ln'(1+0) =1/(1+0)=1
Pour la 2)
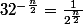
n/2 diverge vers +oo, donc il en est de même pour

. Son inverge converge ainsi vers 0
Pour la 3) , qu'appelles-tu nature d'une suite ?
-
Anonyme
 par Anonyme » 15 Oct 2005, 23:36
par Anonyme » 15 Oct 2005, 23:36
Merci bien Nightmare! Pour la 3°), nature signifie "convergente" ou "divergente".
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 15 Oct 2005, 23:45
par Nightmare » 15 Oct 2005, 23:45
Pour la premiére je te conseil de raisonner par disjonction des cas :

ne peut prendre que 4 valeurs suivant sa nature :
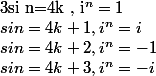
Tu démontreras facilement que dans chaques cas, la suite converge vers 0
Je réfléchis pour la deuxiéme
:happy3:
-
Anonyme
 par Anonyme » 16 Oct 2005, 09:15
par Anonyme » 16 Oct 2005, 09:15

ne peut prendre que

valeurs suivant sa nature :
si

si
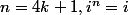
si
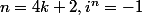
si
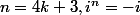
euh... tu dis si
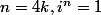
Je ne suis pas d'accord, et dirai plutôt
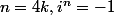
et plus simplement si
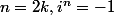
non?
-
Anonyme
 par Anonyme » 16 Oct 2005, 09:21
par Anonyme » 16 Oct 2005, 09:21
Ah non, ce que je viens de dire est totalement faux, autant pour moi ...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 16 Oct 2005, 10:07
par Nightmare » 16 Oct 2005, 10:07
si n=4k :
^{n}=(-1)^{2n}=1)
:happy:
-
Anonyme
 par Anonyme » 16 Oct 2005, 10:13
par Anonyme » 16 Oct 2005, 10:13
Oui oui tout à fait d'accord!
Par contre après je ne vois pas tellement comment poursuivre l'étude..en effet on a une forme indéterminée
)
...
Ou alors je prends les termes du plus haut degré (mais je ne sais pas on a le droit avec le [/tex]i^n[/tex] et alors à chaque cas c'est
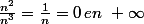
... ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 16 Oct 2005, 10:17
par Nightmare » 16 Oct 2005, 10:17
Justement, il ne faut pas laisser le

tel quel.
Il faut procéder au cas par cas.
Dabord tu prends
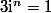
On a :
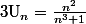
Ca converge vers 0
Avec
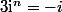
On a :
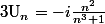
Ca converge vers 0
Etc...
:happy3:
Jord
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 16 Oct 2005, 10:19
par Nightmare » 16 Oct 2005, 10:19
Pour le deuxiéme ça doit surment mettre un cas de divergence du fait des cosinus et sinus mais j'ai un peu du mal à le montrer. J'avous que les suites à valeur dans C ce n'est pas trop mon trip.
:happy3:
-
Anonyme
 par Anonyme » 16 Oct 2005, 10:28
par Anonyme » 16 Oct 2005, 10:28
Oui, c'est en gros ce que je disais! (enfin ce que je pensais, je l'ai mal exprimé je m'en rends compte...) Merci! Et quant à la deuxième suite, tu as une idée?
Rappel:
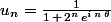
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités