Suites puissances prépa bio

[miumiu78]

bonjour!!
J'ai un dm a rendre pour la semaine prochaine et je coince sur une question
Soit a un réel
Pour tout entier n;)1 on pose Un = (a^n)/n!
et Vn = lUnl = lal^n/n!
1)vérifier que si a =0 , lim+;) Un=0
là ça va c'est pas trop dur
2)
a)pour tout a ;)0
calculer lim+;) V(n+1)/Vn
je trouve 0 je pense que c'est bon
b) en déduire qu'il existe un entier naturel No tel que pour tout n;)No on a V(n+1) ;)(1/2) Vn
bon là déja je bloque un peu j'ai posé Wn = V(n+1)/Vn et j'ai utilisé la définition d'une suite qui tend vers un réel avec ;) = 1/2 mais bon je ne suis pas trop sûre
c) montrer par récurrence que 0;)Vn;)V(No)×(1/2)^(n-No)
et je là bloque dur :cry: je ne voie pas quoi prendre comme terme pour mon initialisation
merci d'avance

[Yipee]

Pour le c) je pense que la récurrence consiste à montrer que pour tout entier n supérieur à N0 on a .... Il faut donc faire l'initialisation à N0

[Zebulon]

Bonsoir,
pour la question 2b, c'est ce qu'il faut faire, mais cette suite ne tend pas vers n'importe quel réel, elle tend vers 0. Mais je suppose que vous l'avez fait correctement.
Pour la récurrence, ce ne serait pas pour ?
Dans ce cas, vous pouvez montrer l'initialisation pour , mais pour comprendre d'où sort cette récurrence, je vous conseille de la montrer (au brouillon) aussi pour 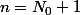et .

[Zebulon]

Un peu de culture
L'an prochain, vous étudierez les séries, et en généralisant un peu, on obtient la démonstration d'une partie de la "règle de D'Alembert".

[miumiu78]

Bonsoir,
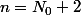pour la question 2b, c'est ce qu'il faut faire, mais cette suite ne tend pas vers n'importe quel réel, elle tend vers 0. Mais je suppose que vous l'avez fait correctement.
Pour la récurrence, ce ne serait pas pour ?
Dans ce cas, vous pouvez montrer l'initialisation pour , mais pour comprendre d'où sort cette récurrence, je vous conseille de la montrer (au brouillon) aussi pour et .

oui en effet on a
merci beaucoup pour votre aide :we: