Suites numériques

[endiaye01]

Bonjour
je cherche à démontrer que pour tout n de N
Un=n^2 diverge en utilisant la définition formelle de la convergence avec epsilon.
Merci d'avance

[GaBuZoMeu]

Bonjour,

Tu peux montrer que cette suite tend vers en utilisant la définition des limites infinies.

[endiaye01]

non en fait l'exercice m'impose de passer par cette méthode
voilà ce que j'ai fait une démonstration par l'absurde dites moi ce que vous en pensez
admettons que la suite Un tend converge vers l>0 ∀ n de N
donc ∀ε >0 il exite N(ε) entier naturel tel que ∀ n>N(ε) implique que |n^2 - l| <ε
Donc -ε<n^2-l <ε
on a n^2 - l > -ε implique que n^2> l - ε qui implique que n> racine carré de ( l-ε) qui représenterai N(ε)
Or ε est positif et quelconque donc on peut trouver un ε>l ce qui voudrait dire que l- ε<0 donc l'existence de sa racine carrée serait absurde
d'ou Un= n^2 n'est pas convergente.
Vous en pensez quoi?

[GaBuZoMeu]

J'en pense que tu te perds dans le formalisme et que ça aboutit à des bêtises.
Tu ne démarres pas trop mal.

Tout de même, une remarque Quand tu écris "la suite Un tend converge vers l>0 ∀ n de N", la quantification universelle sur n n'a aucun sens. En fait, quand tu parles de "la suite Un", il s'agit en fait de la suite et le ici est une variable muette. Tu pourrais le remplacer par , par , ça serait la même chose.

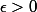
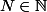
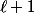
Ensuite tu déroules la définition et tu supposes qu'il existe tel que pour tout il existe tel que pour tout , . OK. Là tu veux montrer que c'est absurde et ça déraille. Revenons au bon sens pour comprendre l'absurdité de cette supposition. Le bon sens nous dit que peut être rendu aussi grand qu'on veut en prenant suffisamment grand. Et en particulier, plus grand par exemple que . D'accord ? Alors garde cette idée en tête et essaie de formaliser. Ne te laisse pas aveugler par le formalisme.

[endiaye01]

Ahh d'accord je vois.
En fait comme l'exercice m'impose de passer par la définition formelle, je n'ai utilisé que les éléments qui se trouvent dans cette dernière.
Et à la fac on nous a habitué à utiliser la définition pour montrer la convergence en cherchant à trouver un Nepsilon adéquat et sa contraposée pour la divergence en cherchant un epsilon adéquat c'est ce que j'ai voulu faire ici mais bon.
Comment je pourrais faire alors pour montrer que Un diverge
un indice?

[GaBuZoMeu]

Je pense t'avoir donné un indice dans mon message ...