Suites homographique

[ArtyB]

Bonjour,
Soit la suite suivant: avec a réel strictement positif et
1/ Etudier sa convergence
2/ On introduit , exprimer en fonction de n et
3/ Montrer que si alors et en déduire une méthode permettant le calcul approché de

1/ La suite converge vers
On le démontre par la décroissance de la suite et le fait qu'elle soit minorée ce qui permet d'en déduire sa convergence.

2/ Démonstration triviale:

3/ Aucune idée mais alors vraiment aucune, et vous ?

[Doraki]

Pour la 3 tu devrais vérifier ton énoncé. A droite t'as un truc qui dépend de n et pas à gauche.

[ArtyB]

Argh au temps pour moi je commence tout juste à découvrir les balise [TEX ] et j'ai fais un copié collé que j'ai oublié de modifier, mea culpa. J'ai modifié.

[paquito]

Si , tu vas avoir

on obtient:


puis , etc; donc ça va très vite; cette méthode s'appelle la méthode de Babylone, ce qui veut dire qu'elle est connue depuis longtemps; on la retrouve facilement avec la méthode de Newton.

[ArtyB]

Chouette c'est ce que j'avais fait au brouillon mais je n'étais pas sûr par rapport aux valeurs absolues.
Je ne connaissais pas cette méthode, c'est puissant ! Ca donne les bonnes décimales jusqu'à très loin ! J'aime tellement les mathématiques, je voudrais passer ma vie à en faire !
Et donc pour trouver une valeur approchée de il faut prendre la limite de en plus l'infini de la suite ?

[Pythales]

Chouette c'est ce que j'avais fait au brouillon mais je n'étais pas sûr par rapport aux valeurs absolues.
Je ne connaissais pas cette méthode, c'est puissant ! Ca donne les bonnes décimales jusqu'à très loin ! J'aime tellement les mathématiques, je voudrais passer ma vie à en faire !
Et donc pour trouver une valeur approchée de il faut prendre la limite de en plus l'infini de la suite ?

Si ça t'intéresse :

Plus généralement, est la limite de la suite

[Ben314]

Tout à fait.
Et le moins qu'on puisse dire, c'est que ça date pas d'aujourd'hui vu que ça s'appelle algorithme de Babylone (ou méthode de Héron) et que ça semble dater de la nuit des temps...
Il y a d'ailleurs une jolie façon de voir géométriquement l'algorithme : on se donne une surface S et on aimerais trouver un carré de coté c ayant pour surface S (donc c²=S).
On part d'un rectangle R de coté uxv de surface S, si possible pas trop loin d'un carré puis on trace un nouveau rectangle R' de cotés u'xv' de même surface S en prenant pour u' la moyenne de u et v (pour que R' soit "plus carré" que R).
Comme u.v=S on a en fait u'=(u+v)/2=(u+S/u)/2.

Sinon, si on veut être un peu plus "récent", on peut aussi y voir un cas particulier de la Méthode des tangentes de Newton


EDIT : j'avais pas lu entièrement le post de paquito dont le mien est un... copié collé...

[ArtyB]

Merci à vous !
C'est génial ça je trouve ! Pourquoi n'en ai-je pas entendu parler plus tôt ?!
Pas de mot pour décrire à quel point j'aime ça, j'ai l'impression d'être comme un enfant devant un nouveau jouet utra moderne.

[Ben314]

Si ça t'amuse, on peut aussi trouver des généralisations "algébriques" de l'algorithme de Babylone :
Essaye par exemple
ou bien

D'où sortent ces formules ?

[paquito]

Je vais en ajouter 2 plus simples à trouver:



et c'est l'occasion d'expliquer la méthode de Newton.

Je considère que est l'unique solution de pour et je sais vérifier que f garde une concavité constante sur un voisinage de et je suis quand même capable de trouver un encadrement d'amplitude de;

Passons au choses sérieuses: soit tel que et étant déterminé, soit le point de la courbe d'abscisse et la tangente àen :

est l'abscisse du point d'intersection de avec l'axe horizontal. Ca donne:

avec

relation qui est générale mais il faut éviter;

On vérifie en général que si 0, et ; donc la méthode s'applique pour la résolution approchée mais rapide de(presque) toute équation.

L'exemple que j'ai donné sert uniquement à illustrer la méthode; je te laisse le soin de l'appliquer pour retrouver la méthode de Babylone qui est plus performante.

Je t'en donne une autre plus performante:

,


Quant au trucs que nous donne Ben pour qu'on ne s'ennuie pas, peut être qu'un jour on aura une explication, qui sait.....

[Ben314]

Oui... mais...
1) Pour la suite définie par où on a et (comme toujours avec la méthode de Newton et cela assure une convergence "rapide") mais on a donc la vitesse de convergence n'est pas vraiment meilleure qu'avec l'algorithme de Babylone "standard" (alors que la formule est plus compliquée).

2) Pour la suite définie par où , là, effectivement, c'est "plus performant" vu que, non seulement et mais aussi donc c'est bien plus rapide.
Sauf que c'est de la triche vu qu'en fait où donc tout ce qu'on a fait, c'est de prendre un terme sur 2 de la suite de Babylone "standard".

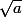
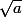
Tu peut vérifier que les deux que j'ai donné sont "plus rapides" que la suite standard : f'=f''=0 en pour la première et f'=f''=f'''=f''''=0 en pour la seconde.
D'où sortent ces formules ?

Indications :
- Pas besoin de connaitre la méthode de Newton
- Je peut t'écrire la suivante (i.e. f'=f''=f'''=f''''=f'''''=0) sans faire aucun calculs.
- Pour toutes ces suites là, on peut exprimer Un en fonction de U0 et de n (à l'aide des fonctions "usuelles")

[paquito]

Si on ne peut pas tricher un petit peu....

[Ben314]

Bon, je donne la réponse qui EST en fait dans l'énoncé de départ (1er post) :
L'énoncé en question considère où
Il suggère ensuite d'étudier où c'est à dire en fait (donc un conjugué de )
On vérifie alors que puis que où .

Si on veut que "ça aille plus vite", ben y'a qu'à remplacer par , c'est à dire prendre :

qu'on peut écrire "sans réfléchir" si on connait la d-ième ligne du triangle de pascal.

Remarque : Par construction même, les fonction vérifient (car ) donc, par exemple, correspond à prendre un terme sur deux dans la suite d'origine
De même correspond à prendre un terme sur trois...
Par contre, je ne vois à priori pas de lien entre et (à part qu'elle commutent) donc à priori pas de lien entre les suites et (si quelqu'un trouve un lien, ça m'intéresse...)

[ArtyB]

Waow euh je viens de lire tout ça j'y re-réfléchirais à tête reposée parce que là j'ai un peu de mal pour tout dire...
Mais merci ! Ca m'a l'air très intéressant !

[paquito]

Salut Ben et merci pour toutes ces précisions,

sinon entre et , on a la relation.je ne sais pas si ça peut conduire à quelque chose.

[Ben314]

Oui, j'avais pas fait gaffe à ça et d'ailleurs, ça marche pour d quelconque et ça se voit immédiatement dans la formule

Mais je suis pas sûr qu'il y ait des propriétés algébriques intéressantes entre et .

[paquito]

Il y a quand même un truc rigolo; si on par de

on a f, puis

puis car puis

Mais si on peut descendre, on peut remonter grâce à la condition.

Exemple, donc à une constante que j'ignore pour l'instant,

;

d'où

On obtient bien sûr aussi facilement de, ou de et si on pose puis = on obtient =

Une belle suite de fonctions