Suites : Un doute

[rifly01]

Bonjour,

Voilà j'ai un doute. Et donc je viens ici pour m'enlever ce doute !


Soit une suite et on lsuppose que ,
Déterminer et

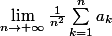
Ma réponse :

On pose :
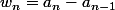
D'après principe de Cesaro :
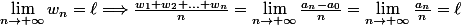
[CENTER][/CENTER]


Il vient :


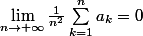
Et on peut même généraliser : Si converge vers
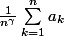
alors pour tout , on a converge vers 0.

Merci d'avance,

[kazeriahm]

ben non a_n/n->l donc encore par Cesaro, ta deuxieme limite est l

[rifly01]

AH oui zut, C'est double cesaro,


Donc je corrige ma petite généralisation :


Et on peut même généraliser : Si converge vers
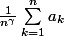
alors pour tout , on a converge vers .

C'est bon cette fois ?

[Babe]

oui a priori c'est bon

edit: je sors :zen:

[kazeriahm]

desolé mais non plus, la généralisation n'est pas bonne,

avec ton exemple 1/n^2*somme(a_n) tend vers l

donc 1/n^3*somme(...) = 1/n * 1/n^2*somme(...) tend vers 0*l=......

EDIT : parcontre tu peux appliquer Césaro autant de fois que tu veux ca ca marchera toujours mais ca te donne pas la généralisation (tu vas obtenir des sommes doubles, triples, etc...)

[kazeriahm]

en fait non la deuxieme limite marche pas par Cesaro, Cesaro ca donnerait :

1/n*somme(a_k/k) tend vers l

ici tu as a_n+1-a_n qui tend vers l

donc quand tu sommes par Cesaro, ca te donne (S_n+1-S_n)/n tend vers l

donc S_n+1 equivaut à n*l+S_n donc en sommant ca (je sais pas si tu sais faire ca, c'est Cesaro detourné, ici il ne s'agit pas limite mais d'équivalent)

on a S_n+1 equivaut à n(n+1)/2*l

donc S_n/n^2 tend vers l/2

je crois ?

[kazeriahm]

oula en fait j'ai dit une betise, ca marche pas Cesaro à la deuxieme... parceque Cesaro ca donnerait

1/n*somme(a_k/k) tend vers l

je crois que la limite c'est l/2 mais faut que je verifie et j'ai pas le temps

[rifly01]

Merci,

Un autre truc je veux faire exister lol,

Soit
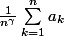
Si converge vers alors pour tout , on a converge vers .

C'est bon cette fois ?

[kazeriahm]

non si gamma = 2 et a_n=n, tu as a_n/n^(gamma-1) qui tend vers 1

et pourtant ta deuxieme suite tend vers 1/2 (limite de n(n+1)/2*n^2

[rifly01]

Merci pour tout !
kazeriahm

[kazeriahm]

de rien j'aurai preferé confirmer à chaque fois :we:

[yos]

Bonsoir.
En supposant 0 :, donc , donc .