Suites définies par récurrence

[Anonyme]

Bonjour !
Dans un exo on me demande de trouver l'expression de an défini par la relation de récurrence :
(n+1) x a indice (n+1)=2 x a indice (n-1)
avec a0=0 et a1=1
Comment faire ? Merci de votre coup de pouce.

[Nicolas_75]

Je comprends :


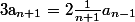
Ecris a0, a2, a4, a6, sans simplifier. L'expression de a(2n) apparaîtra d'elle-même.

Ecris a1, a3, a5, a7, sans simplifier. L'expression de a(2n+1) apparaîtra d'elle-même.

[nuage]

Salut,
une première remarque : on peut considérer la suites des termes de rang pair et celle des termes de rang impairs de façon indépendantes.
Si n est pair la réponse est facile la suite des a_indice(2k) est constante.
Si n est impair on peut utiliser le résultat :

sauf erreur de ma part...

[Anonyme]

Donc je trouve a2n=[2/(2n+1)] x a indice (2n-1)
et a indice 2n+1 = [2/(2n+2)] x a2n

Et après c'est fini ?

[nuage]

Donc je trouve a2n=[2/(2n+1)] x a indice (2n-1)
et a indice 2n+1 = [2/(2n+2)] x a2n

Et après c'est fini ?

C'est pas ce que j'avais compris de ton énnoncé (la même chose que Nicolas_75)
pour n=1 on a : n+1 = 2 ; n-1=0 donc 2 a_2 = 2 a_0 =0 et a_2=0
pour n= 3 on a : n+1 =4 ; n-1=2 donc 4 a_4 = 2 a_2
etc....

[Anonyme]

Euh j'ai pas très bien compris ... En bref, l'expression de an qu'est ce que c'est exactement ?

[nuage]

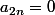
Sauf erreur de ma part pour le 2° résultat.
Tout ceci reste à démontrer en utilisant
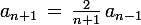
Calcule effectivement les premières valeurs.