Suites complexes périodiques
23 messages
- Page 1 sur 2 - 1, 2
Suites complexes périodiques
Bonjour,
Ma fin de dm de maths pour ces vacances est assez corsée.
Sur une des dernières questions, je dois montrer qu’une suite à valeurs dans l’ensemble des complexes est n-périodique si et seulement si il existe des complexes notés C0, C1,…,Cn-1 tels que:
[img]http://latex.ilemaths.net/ile_TEX.cgi?Uk=\sum_{p=0}^{n-1}{Cp%20\omega^p^k}[/img]
Et il faut aussi montrer l'unicité des complexes C0,...,Cn-1.
En raisonnant par double-équivalence, il y a une implication qui est évidente: en supposant l'existence, la périodicité se montre juste en calculant Un+k.
En revanche, pour montrer que les complexes C0,...Cn-1 existent et sont uniques, en supposant que la suite est périodique, je ne vois pas comment procéder.
Ma fin de dm de maths pour ces vacances est assez corsée.
Sur une des dernières questions, je dois montrer qu’une suite à valeurs dans l’ensemble des complexes est n-périodique si et seulement si il existe des complexes notés C0, C1,…,Cn-1 tels que:
[img]http://latex.ilemaths.net/ile_TEX.cgi?Uk=\sum_{p=0}^{n-1}{Cp%20\omega^p^k}[/img]
Et il faut aussi montrer l'unicité des complexes C0,...,Cn-1.
En raisonnant par double-équivalence, il y a une implication qui est évidente: en supposant l'existence, la périodicité se montre juste en calculant Un+k.
En revanche, pour montrer que les complexes C0,...Cn-1 existent et sont uniques, en supposant que la suite est périodique, je ne vois pas comment procéder.
Re: Suites complexes périodiques
...et je suppose que
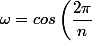+i.sin\left(\dfrac {2\pi }{n}\right))
avec mais bon là je m'avance certainement
mais bon là je m'avance certainement
mais sinon oui c'était bien ça Mathelot
avec
mais sinon oui c'était bien ça Mathelot
Re: Suites complexes périodiques
et si c'est ça alors on a bien la périodicité vu que

Le théorème de Moivre le stipule
Le théorème de Moivre le stipule
Re: Suites complexes périodiques
normalement c'est la convention qu'on a avec la lettre omega
mais peut être que je m'avance (j'ai juste supposé en attendant qu'il vienne)
mais peut être que je m'avance (j'ai juste supposé en attendant qu'il vienne)
Re: Suites complexes périodiques
Pour l'existence des C_i i=0,1,...,n-1 (et leur unicité)
on peut dire qu'elles sont solutions d'un système linéaire de n inconnues et n équations.


..

....
} = u_{n-1})
de déterminant non nul:
https://fr.wikipedia.org/wiki/Matrice_de_Vandermonde
https://fr.wikipedia.org/wiki/Transform ... cr%C3%A8te
on peut dire qu'elles sont solutions d'un système linéaire de n inconnues et n équations.
..
....
de déterminant non nul:
https://fr.wikipedia.org/wiki/Matrice_de_Vandermonde
https://fr.wikipedia.org/wiki/Transform ... cr%C3%A8te
Modifié en dernier par mathelot le 02 Nov 2021, 21:46, modifié 2 fois.
Re: Suites complexes périodiques
Bonsoir,
Il est raisonnable de penser que est une racine primitive
est une racine primitive  -ème de l'unité.
-ème de l'unité.
Il est utile de se rappeler que si
si  divise
divise  , et 0 si
, et 0 si  ne divise pas
ne divise pas  .
.
Les termes
termes  déterminent entièrement la suite périodique.
déterminent entièrement la suite périodique.
Pour trouver les on peut
on peut
- soit penser en termes d'un système linéaire de équations à
équations à  inconnues,
inconnues,
- soit penser en termes de transformée de Fourier, grâce à la propriété rappelée ci-dessus.
Il est raisonnable de penser que
Il est utile de se rappeler que
Les
Pour trouver les
- soit penser en termes d'un système linéaire de
- soit penser en termes de transformée de Fourier, grâce à la propriété rappelée ci-dessus.
Re: Suites complexes périodiques
bah sinon comme je vois le bidule
on peut argumenter le fait que la famille des C_n est finie et comme les puissances d'omega sont périodiques bah du coup la suite est périodique mais ça fait pas propre comme démo mais bon l'idée du bidule quoi
on peut argumenter le fait que la famille des C_n est finie et comme les puissances d'omega sont périodiques bah du coup la suite est périodique mais ça fait pas propre comme démo mais bon l'idée du bidule quoi
Re: Suites complexes périodiques
Oui, désolé j’ai oublié de la rappeler mais oméga sont les racines de l’unité, notées comme e^i(2pi/n)
Re: Suites complexes périodiques
Je dois donc établir établir un système de n équations à n inconnues avec les termes de la suite, prendre les C_i où i va de 0 à n-1 comme racines de cette équation, et c’est tout ? Comme par magie mes C_i apparaissent comme solutions
Re: Suites complexes périodiques
Je ne pense pas que ce soit la peine (je ne pense pas non plus que GaBuZoMeu vous demande de le faire non plus: il ne fait juste que dire comment avoir les termes mais nul part il ne dit qu'il faut les avoir pour démonter la périodicité)
J'ai donné une démo plus haut : elle tient en une ligne et sans calculs
J'ai donné une démo plus haut : elle tient en une ligne et sans calculs
Re: Suites complexes périodiques
azf a écrit:J'ai donné une démo plus haut : elle tient en une ligne et sans calculs
non c'est pas bon!
Mieux vaut calculer les termes comme le suggère GaBuZoMeu
Je ne suis plus du tout convaincu par ce que j'ai dit
Re: Suites complexes périodiques
Donc là pour le coup (ma pseudo démo précédente est plus que merdique)
donc là bah du coup j'ai pensé certes vite fait car cette nuit j'ai pensé à des trucs mais pas vraiment des maths pardon mais des fois je pense à des trucs de mes coutumes (si vous voyez ce que je veux dire ) utiliser la matrice elle est diagonalisable et ses valeurs propres et multiplicités algébrique sont données ci-dessous donc sont facilement calculables même si la matrice est grande car là le degré du degré du polynôme caractéristique ne va pas nous gêner
elle est diagonalisable et ses valeurs propres et multiplicités algébrique sont données ci-dessous donc sont facilement calculables même si la matrice est grande car là le degré du degré du polynôme caractéristique ne va pas nous gêner

}&\omega ^{0\times \left(n-1\right)}&\ldots & \omega ^{0\times \left(n-m\right)}\\ \ldots& \ldots & \ldots & \ldots \\ \omega ^{m\times \left(n-0\right)}&\omega ^{m\times \left(n-1\right)}&\ldots & \omega ^{m\times \left(n-m\right)}\end {pmatrix})

valeurs propres de V
ses valeurs propres sont parmi

avec les multiplicités respectives

et bon après avec ça je pense qu'on peut l'utiliser dans le contexte de la question ici
donc là bah du coup j'ai pensé certes vite fait car cette nuit j'ai pensé à des trucs mais pas vraiment des maths pardon mais des fois je pense à des trucs de mes coutumes (si vous voyez ce que je veux dire ) utiliser la matrice
valeurs propres de V
ses valeurs propres sont parmi
avec les multiplicités respectives
et bon après avec ça je pense qu'on peut l'utiliser dans le contexte de la question ici
Re: Suites complexes périodiques
Est-ce que le fait de dire que les C_i (i dans 0 à n-1) existent car ils sont solutions d’un système comme l’a dit GaBuZoMeu suffit ? Je ne vois pas le lien entre montrer une existence et avoir les valeurs propres et multiplicités respectives de matrices
Re: Suites complexes périodiques
Alex0347 a écrit:Est-ce que le fait de dire que les C_i (i dans 0 à n-1) existent car ils sont solutions d’un système comme l’a dit GaBuZoMeu suffit ? Je ne vois pas le lien entre montrer une existence et avoir les valeurs propres et multiplicités respectives de matrices
non pas de matrices mais de la matrice V
sinon il y a combien de coefficients C_i ? il y en a n de C_0 à Cn-1
vous avez là le vecteur colonne composée des C_i
un produit à faire avec une matrice (la matrice V) pour avoir un système d'équation linéaire
en plus un système de Kramer (donc une solution unique : le vecteur colonne que vous recherchez)
Moi comme je vois la chose il faut diagonaliser la matrice V et s'en servir mais j'avoue que pour l'instant je n'ai pas encore réfléchi au problème (j'ai juste lu GaBuZoMeu et j'essaye juste de voir en gros ce qu'il dit)
Re: Suites complexes périodiques
de toute façon vous ne pouvez pas vous servir de la matrice V
il faut vous servir de la matrice diagonale de votre diagonalisation sinon vous n'aurez pas vos produits donnés dans votre premier post
mais c'est pas grave elle est simple à diagonaliser vu que vous avez tout ce qu'il faut
les valeurs propres et leurs multiplicités algébriques respectives
En ce qui me concerne je n'ai pas encore réfléchi à la question mais bon vu en gros comme ça c'est l'idée que je me fais du comment on doit s'y prendre mais maintenant si vous pensez que c'est pas bon ah bien j'avoue que j'ai rien fait donc il est fort probable que je me trompe (ça ne serait pas la première fois que je raconte des conneries sur des intuitions d'idées en gros du comment aborder un problème mais sans avoir commencé à le faire pour de bon mais je ne pensais pas que je devrai le faire en entier mais juste lancer une idée et voir si ça colle de près ou de loin avec celle des autres )
il faut vous servir de la matrice diagonale de votre diagonalisation sinon vous n'aurez pas vos produits donnés dans votre premier post
mais c'est pas grave elle est simple à diagonaliser vu que vous avez tout ce qu'il faut
les valeurs propres et leurs multiplicités algébriques respectives
En ce qui me concerne je n'ai pas encore réfléchi à la question mais bon vu en gros comme ça c'est l'idée que je me fais du comment on doit s'y prendre mais maintenant si vous pensez que c'est pas bon ah bien j'avoue que j'ai rien fait donc il est fort probable que je me trompe (ça ne serait pas la première fois que je raconte des conneries sur des intuitions d'idées en gros du comment aborder un problème mais sans avoir commencé à le faire pour de bon mais je ne pensais pas que je devrai le faire en entier mais juste lancer une idée et voir si ça colle de près ou de loin avec celle des autres )
Re: Suites complexes périodiques
azf, tu crois vraiment aider le questionneur avec ton flot de messages plus ou moins pertinents (plutôt moins que plus, d'ailleurs) ?
Pour voir ce qu'il y a derrière cet exercice, on peut chercher dans wikipedia avec la requête "Transformation de Fourier discrète".
Pour voir ce qu'il y a derrière cet exercice, on peut chercher dans wikipedia avec la requête "Transformation de Fourier discrète".
23 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
