Suite

[Salamèche51100]

soit la suite (un) définie par : °u0 appartient à ]0;1[
° Pour tout n appartenant à N, un+1=f(un)
où f est la fonction définie sur R par f(x)=x(1-x).

J'ai réussi pas mal de question mais je bloque à partir de là :
On pose wn=n*un
(a) montrer que (wn) est croissante et qu'elle converge
Là j'ai expliqué que la suite (un) converge et qu'elle était croissante par conséquent la suite (wn) l'est aussi.

Et a partir de là ça se complique :
(b)on note L= lim n--> + inf (wn) . montre que L apartient à ]0;1[.

(c) on pose vn=n(wn+1-wn)
montrer que pour tout n appartenant à N, vn=wn(1-wn-un)
En déduire que vn converge et déterminer sa limite en fonction de L

MERCI d'avance pour votre aide :)

[arnaud32]

tu peux nous montrer ce qu'il y a avant? car est decroissante et converge vers 0
sinon regardes et

[BiancoAngelo]

Bonjour, déjà je préfère réécrire tout ça en latex pour y voir plus clair

Soit la suite définie par :

où est la fonction définie sur par .

On pose
(a) Montrer que est croissante et qu'elle converge
(b) On note . Montrer que .

(c) On pose .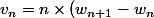
Montrer que pour tout n appartenant à N, .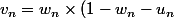
En déduire que converge et déterminer sa limite en fonction de .

[BiancoAngelo]

(a) montrer que (wn) est croissante et qu'elle converge
Là j'ai expliqué que la suite (un) converge et qu'elle était croissante par conséquent la suite (wn) l'est aussi.

Par conséquent, la suite est quoi ? Croissante, convergente ?
D'ailleurs, la suite n'est pas croissante, et le "par conséquent" est faux.

Si une suite tend vers 1, cette suite "fois n" tend vers l'infini...

[Salamèche51100]

1) (a) étudier les variations de f sur R.
(b) Déterminer f(]0,1[)
(c) montrer que si n \in N, f(1/n+1)<(1/n+2)
(d) Montrer par récurrence que pour tout n \in N*, 0(e) en déduire que (un) converge et déterminer sa limite



Voilà ce qu'il y avait avant

[Salamèche51100]

Mais la suite (un) ne tend pas vers 1 puisqu'elle est comprise entre 0 et 1/n+1
Donc par encadrement la suite tend vers 0 et non vers 1

[BiancoAngelo]

Mais la suite (un) ne tend pas vers 1 puisqu'elle est comprise entre 0 et 1/n+1
Donc par encadrement la suite tend vers 0 et non vers 1

Oui mais c'est un exemple que je donnais.
C'est pas non plus parce qu'une suite tend vers que 0 "fois n", elle convergera.

Prends la suite des qui tend bien vers 0, et pourtant, tend vers l'infini.

[Salamèche51100]

D'accord j'ai compris donc on a bien notre suite (un) qui converge et plus précisément elle tend vers 0 et comme u0 appartient à l'intervalle ]0;1[ on en déduit qu'elle est décroissante ?

[BiancoAngelo]

D'accord j'ai compris donc on a bien notre suite (un) qui converge et plus précisément elle tend vers 0 et comme u0 appartient à l'intervalle ]0;1[ on en déduit qu'elle est décroissante ?

Fais les choses posément. Une suite peut tendre vers 0 et être positive sans être décroissante.

La suite définie par : tend bien vers 0 et pourtant change de variations.

Bref, d'après la première question, tu as étudié .
Étudie les variations de f, et pour , tu pourras démontrer alors que ta suite est décroissante par récurrence. Proprement ! :lol3:

EDIT : En supposant que montrer que cette suite est décroissante soit vraiment important.

[Salamèche51100]

oui c'est vrai je m'égard puisqu'on me demande uniquement la convergence ainsi que sa limite.
Je connais déjà la limite donc la question est faites

[BiancoAngelo]

Si tu as montré que ?

Et du coup apparaît...! Au moins, on aura la majoration.

Ensuite, comme l'a dit Arnaud, calcule et montre que c'est supérieur à 1 pour montrer que cette suite est croissante.

Sachant que tu as l'encadrement de .

[Salamèche51100]

Exact je vais faire ça et je reviens vers vous pour vous montrez ce que j'ai fais.
Merci beaucoup

[Salamèche51100]

Bonjour,
Donc j'ai procéder de la manière suivante:

0 0 0 1
Sachant que bn=n*an

Il vient : (((n+1)*un+1)/(n*un)) > 1
(un+1)/(n*un) > 1/(n+1)
un+1/un > n/n+1

Ce qui peut donné un nouvel encadrement :

wn < n/(n+1) < un+1/un


Remarque: on voit l'apparition de (un+1)/(un) qui est l'étude de la suite (un)

[arnaud32]

tu as

w est donc croissante et majoree donc convergente tu en deduis en plus que

[Salamèche51100]

tu as

w est donc croissante et majoree donc convergente tu en deduis en plus que

On peut donc en déduire que L appartient à ]0;1[

Mais pour la suite on a vn=n(wn+1-wn)
Montrer que vn=wn(1-wn-un)

Ici j'ai essayé de tout développé pour voir si quelque chose de bien apparaissait mais rien de bon pour l'instant une idée ?

[arnaud32]

non juste ]0,1] car le passage a la limite te donne des inegalites larges et non strictes.

j'ai d'ailleurs l'impression que L peut atteindre la valeur 1, est tu sure de ton intervalle?

[Salamèche51100]

oui je suis sûr de mon intervalle c'est bien ]0;1[

[arnaud32]

si tu prends
tu peux trouver tel que et pour tout (ca se montre par recurrence)
tu en deduis que
tu passes a la limite sur n et obtiens et ce pour tout donc

[Salamèche51100]

D'accord, il ne me reste donc plus qu'à prouvez la récurrence de la première ligne je vais essayé merci :)

[Salamèche51100]

[quote="arnaud32"]tu as

w est donc croissante et majoree donc convergente tu en deduis en plus que [TEX]0 1
(un+1)/(un*n) > 1/(n+1)
(un+1)/(un) > n/(n+1)

Ce qui ne m'apporte pas beaucoup d'information sur la convergence de wn mais je voulais simplement savoir comment vous passez de wn+1/wn = ((n+1)/n)*(1-un) ?