Suite/série

par **Mike_51** » 29 Mai 2006, 19:18

Bonjour. J'ai un peu de mal pour cette question de fin d'exo:
Pour tout n, Un>0 et Wn=1/(produit de 1 à n des 1+Uk).
On sait que limWn=L avec L positif ou nul (car (Wn) décroissante minorée par 0).
Je cherche à montrer que L=0 <=> la série des Uk diverge.

par **abcd22** » 29 Mai 2006, 19:40

Bonsoir !
Si Uk tend vers 0 tu peux le montrer en composant avec le logarithme et en prenant un équivalent.
Si Uk ne tend pas vers 0, on peut écrire

, et on utilise ça pour montrer que

,

pour n assez grand.

par **yos** » 29 Mai 2006, 21:53

Je reprends l'idée de abcd22 :

.
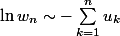
A partir de là, nul besoin de epsilon. (Si L=0, le premier membre va vers -infini, donc la série du second membre diverge. Sinon la série converge.)

par **abcd22** » 30 Mai 2006, 14:10

Le problème, c'est qu'on a l'équivalent

seulement si

tend vers 0, si on prend une suite constante non nulle par exemple c'est faux.

par **yos** » 30 Mai 2006, 20:29

Tu as raison mais on peut faire ça :

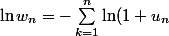. Si Un ne tend pas vers 0, alors

non plus, donc le second membre tend vers - l'infini et donc

.

par **abcd22** » 31 Mai 2006, 15:16

Ah oui c'est plus simple comme ça en effet.

Suite/série

Suite/série

Qui est en ligne