Suite de réels

[Maths-ForumR]

Un = (a0.q^K)/2^(n-k) ?

[capitaine nuggets]

Ton résultat n'a pas de sens...
Pourquoi et ? ne dépendra plus de : c'est une variable relative à la somme :++:

D'ailleurs, j'avais pas bien vu, mais tu n'as pas bien répondu à ma question :

Pour la 4)
Etant donné une suite géométrique de premier terme et de raison , quelle est la formule qui te donne ?

C'est la formule : (1-r^(n+1))/(1-r)

C'est faux, on a si (il faudra bien préciser ça).

Revenons à notre exo : tu as et je constate que la formulation de cette somme ne te plait pas trop. Pas grave, transformons-la. On a aussi :

[CENTER]
[/CENTER]

Pour mieux voir, posons et les suites définies par et . On a alors :

[CENTER].[/CENTER]

En justifiant que est bien une suite géométrique dont on précisera le premier terme 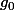et la raison , tu en déduiras puis en fonction de et .

[Maths-ForumR]

Je ne comprend pas comment calculer alors que nous n'avons aucunes indications sur les 1er termes comme par exemple a0

[capitaine nuggets]

Je ne comprend pas comment calculer alors que nous n'avons aucunes indications sur les 1er termes comme par exemple a0

Ok, c'est pas grave. Reprenons tout à zéro :we:

Tu as où est une suite géométrique strictement positive de premier terme et de raison .

On peut réécrire cette somme de la manière suivante .

Posons alors et deux suites respectivement définies par et .

On a alors

- Montre que la suite est géométrique en précisant son premier terme et sa raison.
- En utilisant la formule pour calculer des sommes de termes consécutifs de suites géométriques, montre que :

[CENTER] si

si [/CENTER]

- Déduis-en alors en fonction de , et :+++: