Suite réelle

[jonses]

Bonjour ou bonsoir,

Voilà je bloque complétement sur cet exo :

Soit une suite réelle telle que :

Montrer que la suite est bornée, puis montrer qu'elle est convergente.


J'ai réussi à montrer qu'elle est bornée, mais pour la convergence je suis vraiment bloqué.

Svp si quelqu'un peut m'aider, je le remercie d'avance.

[Archibald]

Bonsoir,

[jonses]

Bonsoir,

Désolé, mais je ne vois pas du tout comment procéder en utilisant cette équivalence

[Ben314]

Deux deux choses l'une :
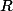
- Soit tu a vu ce qu'est une "suite de cauchy" et le fait que " est complet" et... c'est le moment de t'en servir...
- Soit tu ne l'a pas vu et... ça va franchement être long comme exercice...

[jonses]

Deux deux choses l'une :
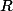
- Soit tu a vu ce qu'est une "suite de cauchy" et le fait que " est complet" et... c'est le moment de t'en servir...
- Soit tu ne l'a pas vu et... ça va franchement être long comme exercice...

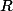
Je n'ai pas vu en cours ce que c'est une suite de cauchy (même si je me suis déjà un petit peu renseigné dessus), mais " est complet" je ne sais pas du tout ce que c'est

[Ben314]

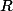
Le fait que " est complet" c'est une façon un peu technique de dire que les suites de cauchy de nombres réels sont forcément convergente.
Ici, la seule façon "raisonnable" (i.e. en moins de 4 pages...) que je vois de faire l'exercice, c'est de montrer que la suite en question est une "suite de cauchy" (c'est quasi la même chose que pour montrer qu'elle est bornée). Puis d'en déduire qu'elle est convergente.

A la limite, on peut aussi utiliser la notions de "séries convergentes" et de "séries absolument convergentes" (le théorème à utiliser reste au fond le même, mais c'est une façon un peu différente de s'exprimer)

[jonses]

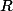
Le fait que " est complet" c'est une façon un peu technique de dire que les suites de cauchy de nombres réels sont forcément convergente.
Ici, la seule façon "raisonnable" (i.e. en moins de 4 pages...) que je vois de faire l'exercice, c'est de montrer que la suite en question est une "suite de cauchy" (c'est quasi la même chose que pour montrer qu'elle est bornée). Puis d'en déduire qu'elle est convergente.

A la limite, on peut aussi utiliser la notions de "séries convergentes" et de "séries absolument convergentes" (le théorème à utiliser reste au fond le même, mais c'est une façon un peu différente de s'exprimer)

Bon je vais essayer de montrer que c'est une suite de cauchy (mais je promets rien).

Je n'ai pas encore vue les séries

Merci en tout cas :lol3:

Je confirme, c'est dur (pour moi)

[jonses]

Merci en tout cas :lol3:

Je confirme, c'est dur (pour moi)

Est-ce qu'il faut que j'essaye d'encadrer par deux suites adjacentes ?
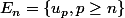
Est-ce que pour faire ça il faut que j'introduise un ensemble du type ? (en tout cas, j'ai essayé, mais j'ai pas l'impression que ça aboutit quelque part)

[jonses]

Est-ce que ce raisonnement est à votre avis valable ? :

, tel que

On dispose de tel que pour tout :



On dispose de tel que pour tout :

alors et donc :



Donc

Donc et sont adjacentes. Elles convergent alors vers la même limite L.

Or donc

[jonses]

Est-ce que ce raisonnement est à votre avis valable ? :

, tel que

On dispose de tel que pour tout :



On dispose de tel que pour tout :

alors et donc :



Donc

Donc et sont adjacentes. Elles convergent alors vers la même limite L.

Or donc

Comment est-ce que je peux faire pour changer le raisonnement pour qu'il soit correct ?

[mrif]

On dispose de tel que pour tout :

N dépend de donc de n

[jonses]

N dépend de donc de n

Ok merci

Donc en fait tout est faux :mur:

Là je vois pas du tout comment procéder

[mrif]

Ok merci

Donc en fait tout est faux :mur:

Là je vois pas du tout comment procéder

Je te propose de creuser cette idée:
Soient m et M respectivement l'inf et le sup de l'ensemble .
Il faut chercher à démontrer qu'à partir d'un certain rang tous les termes de la suite sont soit tout près de m soit tout près de M.

[jonses]

Je te propose de creuser cette idée:
Soient m et M respectivement l'inf et le sup de l'ensemble .
Il faut chercher à démontrer qu'à partir d'un certain rang tous les termes de la suite sont soit tout près de m soit tout près de M.

Merci !

Mais je pense que je vais laisser tomber cet exo (je suis resté trop longtemps dessus, sans résultat)

[Anneauprincipal]

Bonjour,

Je pense qu'il est plus simple d'extraire une sous-suite convergente de , vu qu'elle est à valeur dans un compact. Si il faut justifier cela et bien il faut revenir à la démonstration du théorème de Bolzano-Weierstrass, en procédant par dichotomie.

Parce qu'une fois que tu as une sous-suite convergente , tu peux étudier



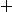
Or cette dernière somme se calcule et tend vers 0 si tend vers , et dans ce cas est proche de la limite de , donc aussi.

Je reste volontairement peu précis pour que tu reprennes cette idée à ton compte si elle te convient.

[mrif]

Merci !

Mais je pense que je vais laisser tomber cet exo (je suis resté trop longtemps dessus, sans résultat)

L'idée que je t'avais suggérée dans mon message précédent ne marche pas car la limite n'est pas nécessairement l'une des bornes.

Contre exemple:
u0= -1/2 et pour n>= 1 un = 1/(2^n).
Cette suite vérifie bien les hypothèses.

Les bornes inf et sup sont -1/2 et 1/2 et sa limite est 0

[Maxmau]

Bonjour ou bonsoir,

Voilà je bloque complétement sur cet exo :

Soit une suite réelle telle que :

Montrer que la suite est bornée, puis montrer qu'elle est convergente.


J'ai réussi à montrer qu'elle est bornée, mais pour la convergence je suis vraiment bloqué.

Svp si quelqu'un peut m'aider, je le remercie d'avance.

Bj
Sans Cauchy ni série

Posons Vn = Un - U(n-1)
V0 + V1 + …….. + Vn = Un - U0
|V0| + |V1| + ……… + |Vn| 0 et zéro sinon
Tn = -Vn si Vn 0 , Wn + Tn = |Vn| , Wn - Tn = Vn
W0 + W1 + ……+ Wn < 2
T0 + T1 + …….. + Tn < 2
Les suites de terme général W0 + W1 + ……+ Wn et T0 + T1 + …….. + Tn sont croissantes majorées. Elles convergent.
Leur différence converge. La suite de terme général V0 + V1 + …….. + Vn = Un - U0 converge et donc la suite (Un) converge

[Ben314]

O.K. pour le "sans cauchy", mais le "sans séries" est un peu "capillotracté"...

La suite de terme général |V0| + |V1| + ……… + |Vn| ...
Les suites de terme général W0 + W1 + ……+ Wn et T0 + T1 + …….. + Tn sont ...

C'est vrai que tu n'utilise pas le mot "séries", mais si c'est juste pour écrire à chaque fois à la place de "série" les mots "suite de terme général ?0+?1+...+?n", je sais pas si ça vaut vraiment le coup.
Il me semble quand même que ce que tu prouve, si on veut le résumer rapidement, c'est que :
"Si une série converge absolument (dans R) alors elle converge"

[Maxmau]

O.K. pour le "sans cauchy", mais le "sans séries" est un peu "capillotracté"...

C'est vrai que tu n'utilise pas le mot "séries", mais si c'est juste pour écrire à chaque fois à la place de "série" les mots "suite de terme général ?0+?1+...+?n", je sais pas si ça vaut vraiment le coup.
Il me semble quand même que ce que tu prouve, si on veut le résumer rapidement, c'est que :
"Si une série converge absolument (dans R) alors elle converge"

Je n'avais d'autre but que de proposer un raisonnement simple accessible à un étudiant qui connait seulement les suites (sans Cauchy) et qui ne connait pas les séries. L'étudiant qui n'a pas vu les séries comprend parfaitement ce qu'est la suite de terme général V0 + V1 +......+ Vn.
Bien entendu, si on connait Cauchy ou le fait qu'une série AC est C, la solution est immédiate.
bonne journée.