Bonsoir,
Voila, j'ai un sale exercice a résoudre sur les suites... Je ne dois pas bien comprendre le problème de la récurrence, sans doute, donc je me réfère à vous.
C'est un cours de math de 1ere à l'université.
Donc... On considère la suite (Un)n appartenant à l'ensemble des nombres naturels.
U0 = 1,
Un+1 = Un + 1/Un
Je dois montrer que pour tout n appartenant à l'ensemble des nombres naturels, que Un est supérieur ou égal à 1, et donc que la suite est bien définie...
Voila, je dois prouver cela par récurrence...
Donc, dans un premier temps, ej remplace n par 0, c'est bien ça? Ce qui me donne 1.
Ensuite, dans un deuxième temps, je dois remplacer n par n+1 et c'est justement là que je bloque, je ne vois absolument pas comment le prouver! J'ai beau tourner cela dans tous les sens, une piste?...
:briques:
Suite récurrente
5 messages
- Page 1 sur 1
C'est le bon mode de raisonnement, tu fais une récurrence sur n pour montrer la propriété:
pour tout n, u(n) supérieur ou égal à 1
initialisation:
Pour n=0, U0=1 donc la propriété est vérifiée
Hérédité, on suppose la propriété vraie a un rang n
On a u(n+1)=u(n)+1/u(n), d'après l'HR u(n) supérieur ou égal à 1 donc 1/u(n) compris entre 0 et 1 et la somme est supérieure à 1.
Voila tout
pour tout n, u(n) supérieur ou égal à 1
initialisation:
Pour n=0, U0=1 donc la propriété est vérifiée
Hérédité, on suppose la propriété vraie a un rang n
On a u(n+1)=u(n)+1/u(n), d'après l'HR u(n) supérieur ou égal à 1 donc 1/u(n) compris entre 0 et 1 et la somme est supérieure à 1.
Voila tout
En effet, il faut commencer par comprendre ce qu'est un raisonnement par récurrence.
Il faut d'abord énoncer une propriété, qui dépend d'un paramètre
qu'on note)
ensuite il faut montrer que pour une première valeur de (en général 0 ou 1)
(en général 0 ou 1)
) est vraie
est vraie
Enfin il faut montrer que si pour une valeur de
) est vraie alors
est vraie alors ) l'est aussi
l'est aussi
Dans ton exemple,
la propriété) est
est 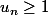
Il faut ensuite montrer)
facile car comme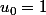 on bien
on bien 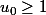
Ensuite montrer que si) est vraie
est vraie
alors) l'est aussi.
l'est aussi.
On suppose donc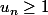
On a alors et donc
et donc 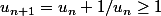
Il faut d'abord énoncer une propriété, qui dépend d'un paramètre
qu'on note
ensuite il faut montrer que pour une première valeur de
Enfin il faut montrer que si pour une valeur de
Dans ton exemple,
la propriété
Il faut ensuite montrer
facile car comme
Ensuite montrer que si
alors
On suppose donc
On a alors
Ok, j'ai vraiment bien saisi tout l'exercice, je sais déjà que la suite est définie, cependant, je n'arrive toujours pas à le démontrer avec le n+1... :mur:
Vous avez des exemples de suites dont on démontre une propriété par récurrence? (suite croissante par exemple), ça m'aidera a y voir plus clair à partir de l'étape de la démonstration avec le n+1
En passant, c'est bien : Un+(1/Un)
Vous avez des exemples de suites dont on démontre une propriété par récurrence? (suite croissante par exemple), ça m'aidera a y voir plus clair à partir de l'étape de la démonstration avec le n+1
En passant, c'est bien : Un+(1/Un)
Quand tu veux démontrer une propriété P(n) avec une récurrence (faible ou forte), tu dois d'abord vérifier que P(0) est vraie comme tu l'as fait.
Ensuite tu prends pour hypothèse P(n) vraie (pour la récurrence faible) et tu te propose de démontrer que P(n+1).
Dans ton exercice quelle est cette hypothèse dite hypothèse de récurrence? C'est
P(n) : Un >= 1
Et la conclusion que tu veux c'est
P(n+1) : Un+1 >= 1
Ensuite tu prends pour hypothèse P(n) vraie (pour la récurrence faible) et tu te propose de démontrer que P(n+1).
Dans ton exercice quelle est cette hypothèse dite hypothèse de récurrence? C'est
P(n) : Un >= 1
Et la conclusion que tu veux c'est
P(n+1) : Un+1 >= 1
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
