Suite récurrente

[Maverick]

Soit S l'ensemble des suites réelles vérifiant Un+1=(Un)²/(n+1).
On note la U(x) la suite de S dont le premier terme est U0=x, x réel.

1) Montrer que la seule limite possible d'une suite U de S est 0.

2) Montrer que x=> Un(x) est continue sur R+.

[klevia]

Attention, ceci est un énoncé en liberté ... Il ne semble appartenir à personne car sinon cette personne nous aurait sans doute saluer et mit quelques mots de politesse ...
Ca fait peur des sujets comme ça qui se balladent tout seuls !!!!

[Maverick]

Okay é bien je remercie d'avance ceux qui aurons l'amabilité de se pencher sur mon problème! Ca te convient?

[Joker62]

ça semble tellement sincère tout ça ! :)

[klevia]

Oui, ca me convient ... un peu .
Soit U une suite de S qui converge vers l différent de 0.
On a : lim [U(n+1)-Un]=0
lim ( )=0
lim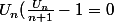
or Un CV vers l donc forcément
lim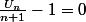

je te laisse finir ...

[Maverick]

lim Un=n+1 elle diverge ce qui en contradiction avec la limite l. trés beau raisonnement par l'absurde mademoiselle; mille remerciements.

[kazeriahm]

lim Un=n+1

ca veut rien dire

[Maverick]

ouais je sais. il fodrait mieux dire se comporte comme n++1 non?
Sinon personne d'autre qui aurait le courage d'affronter la question 2?

[kazeriahm]

bah non mais la contradiction vient du faitr que U_n tend vers l fini non nul donc U_n/n+1 tend vers 0 et -1=0 (donc tu es dieu car si -1=0 alors 1=2 et l'ensemble {Maverick, Dieu} contient {maverick} mais ces deux ensembles ont meme caridnaux donc sont égaux donc Dieu existe et c'est toi)

pour la 2 la question c'est montrer que pour tout n, x->U_n(x) est continue ?

[Maverick]

oui c'est ça

[klevia]

Cela se fait par récurrence ... très facilement en utilisant les théorème de composition, somme ...etc des fonctions continues

[Maverick]

ba lance toi si tu te sent prête

[kazeriahm]

bah c'est évident pour n=0, si c'est vrai au rang n, ie x->U_n(x) est continue sur R, alors U_n+1(x)=u_n(x)^2/n+1 définie clairement une fonction continue sur R

[klevia]

Ok je te le fais...
U0 = x pour tout x appartenant à IR est clairement continue...
Pour tout n , supposons Un continue alors Un+1(x)=Un(x)²/(n+1)
est continue car comme composé de fonction continue :X->X²/(n+1) est continue et Un aussi.
ET voila: facile ...

[Maverick]

Ok merci bien!!!

[kazeriahm]

ensuite on peut peut etre se demander si la fonction x->U est continue pour certaines normes sur l'espace des suites (par exemple si U(x) converge, U est bornée, on peut considèrer le sup |u_n(x)|...) mais je sais pas si c'est interessant

[aviateurpilot]

just une petite remarque hors de l'exercice,

[hicham1979]

bonjour,
aviateurpilot en applicant ta formule pour n=3, le numérateur me parait étrange.
Tu es sûr de ta formule? Peut-être est-ce moi qui fatigue.
Bonne soirée :we:

[hicham1979]

euh le dénominateur pardon...
Je dois être fatigué désolé.