[Défi] Suite récurrente.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 14 Aoû 2010, 18:00
par girdav » 14 Aoû 2010, 18:00
Bonjour,
on définit la suite
_n)
par
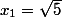
et
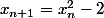
pour tout entier

. Trouver
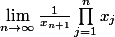
.
Bon courage!
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 14 Aoû 2010, 18:59
par Finrod » 14 Aoû 2010, 18:59
Meuh non c'est simple.
je trouve zéro si
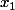
est plus grand que 1. l'infini s'il est plus petit et en 1...
Comme tu l'as posé égal à racine de 5, je vais laisser ça de côté.
(exceptionnellement je suis certain du résultat)
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 14 Aoû 2010, 19:00
par girdav » 14 Aoû 2010, 19:00
Je suppose que tu utilises la trigonométrie hyperbolique.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 15 Aoû 2010, 17:15
par girdav » 15 Aoû 2010, 17:15
Si
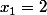
alors on a par récurrence que
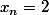
pour tout entier

. Le rapport en question vaut dans ce cas
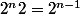
et la limite est bien sûr infinie.
On regarde dans le cas où
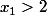
: on pose
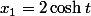
pour un certain

et on peut expliciter

donc le rapport.
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 15 Aoû 2010, 19:07
par Finrod » 15 Aoû 2010, 19:07
Non j'utilisais juste des polynômes.
mais les équivalents que je voulais utiliser sont faux. Je pensais que comme

était un polynôme en
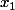
, il pouvait être équivalent au terme de plus haut degrès.
En gros, c'est n'importe quoi.
Je me demande pourquoi j'essaie à chaque fois de faire ces exo, je sais que je ne sais pas faire ces trucs là.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 16 Aoû 2010, 10:14
par benekire2 » 16 Aoû 2010, 10:14
Comme (x_n) diverge, l'étude de cette suite sert pas a grand chose en elle même donc je pense que ça doit être plus dur que ça.
Cela dit, je vais d'abord conjecturer le résultat ( c'est fait, c'est 1) et peut être que la preuve sera plus facile, comme ça arrive souvent sur ce genre d'exos.
EDIT: Je n'avais pas lu le post de Girdav ...
 par busard_des_roseaux » 16 Aoû 2010, 10:19
par busard_des_roseaux » 16 Aoû 2010, 10:19
bonjour,
sinon écrire le quotient de 2 produits successifs
comme (x_n) converge, ces produits se comportent asymptotiquement
comme une progression géométrique
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 16 Aoû 2010, 10:25
par benekire2 » 16 Aoû 2010, 10:25
busard_des_roseaux a écrit:comme (x_n) converge, ces produits se comportent asymptotiquement
comme une progression géométrique
Salut des busard, sauf erreur, (x_n) ne converge pas et diverge en l'infini.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 16 Aoû 2010, 14:02
par girdav » 16 Aoû 2010, 14:02
Pour ceux qui ont trouvé la limite du rapport en question avec
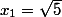
(pas seulement de façon empirique, mais avec une justification), on peut s'amuser à chercher la limite de ce même rapport en fonction de

.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 16 Aoû 2010, 20:05
par girdav » 16 Aoû 2010, 20:05
D'ailleurs, on voit que si on change

en
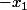
, la suite
)
ne change pas et le rapport non plus.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 20 Aoû 2010, 16:34
par girdav » 20 Aoû 2010, 16:34
Petite remontée d'un topic qui semble sombrer dans l'oubli.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 23 Aoû 2010, 14:05
par Pythales » 23 Aoû 2010, 14:05
Je n'oublie pas...
La difficulté semble être le caractère "pointu" de la convergence.
Une remarque à tout hasard :
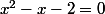
a des racines simples ...
 par busard_des_roseaux » 23 Aoû 2010, 14:43
par busard_des_roseaux » 23 Aoû 2010, 14:43
benekire2 a écrit:Salut des busard, sauf erreur, (x_n) ne converge pas et diverge en l'infini.
Oui, tu as raison.je me suis planté , j'ai regardé la bissectrice avant la courbe :hum:
)
tend en croissant vers l'infini (cf dessin)
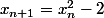
le (-2) est peanuts face à l'infini
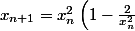)
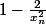
tend vers 1 en croissant
à partir d'un certain rang m fixé
 < x_{n+1}< x_n^2)
d
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 23 Aoû 2010, 16:21
par Pythales » 23 Aoû 2010, 16:21
Le 2 est effectivement peanuts, mais s'il varie d'un epsilon, la limite n'est plus 1...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 23 Aoû 2010, 16:47
par girdav » 23 Aoû 2010, 16:47
On pose
 =x^2-2)
.
 = 4\cosh^2 t-2 = 2\cosh(2t))
.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 23 Aoû 2010, 17:18
par Pythales » 23 Aoû 2010, 17:18
Effectivement, c'est simple :
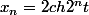
soit
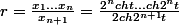
avec
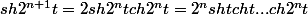
soit
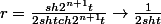
avec
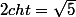
soit
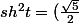^2-1)
et
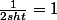
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 23 Aoû 2010, 17:27
par girdav » 23 Aoû 2010, 17:27
Ceci permet de régler le cas où le terme initial est strictement supérieur à

.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Aoû 2010, 23:02
par Ben314 » 23 Aoû 2010, 23:02
Salut,
En fait, on peut procéder de même si
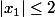
en utilisant des complexes (la fonction Ch est surjective de C dans C).
On peut aussi se passer de trigo hyperbolique (mais ça revient quasi au même) :
Si

et

sont les racines (réelles ou complexes) de
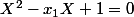
alors, pour tout

, on a
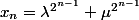
et, si
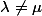
(
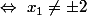
),
x_1x_2...x_n=\lambda^{2^n}-\mu^{2^n})
.
On a donc

- Si
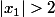
alors

et

sont réels distincts et (par exemple)
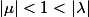
.
On a donc

- Si
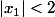
alors

et

sont complexes conjugués et de module égaux à 1 :
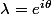
et
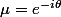
où

est tel que
=\frac{x_1}{2})
.
On a donc
)
et
}\times\frac{\sin\big(2^n\theta\big)}{\cos\big(2^n\theta\big)})
dont les comportements lorsque
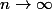
dépendent de la valeur initiale...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 24 Aoû 2010, 20:16
par girdav » 24 Aoû 2010, 20:16
Je n'avais pas pensé à cette méthode.
Le problème initial consistait à traiter seulement le cas où
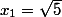
et est tiré des IMC.
Il est vrai que le cas où
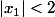
est plus difficile.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 25 Aoû 2010, 13:53
par Pythales » 25 Aoû 2010, 13:53
En fait, si
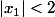
il suffit de reprendre le message 16 et de remplacer le
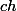
par
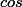
On arrive à la même conclusion que Ben314.
Le cas
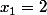
est trivial.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités