Suite de polynôme
23 messages
- Page 1 sur 2 - 1, 2
Suite de polynôme
Bonjour, voici l'exercice sur lequel je suis bloquée, la c) et à partir de la e)
P0 = 1
Pn+1 = 2XPn- 1/(n+1) * (1+X²)P'n
a) Calculer P1 et P2
P1 = 2X et P2 = 3X²-1
b) Montrer que le degré de Pn est inférieur ou égal à n
J'ai fait une récurrence
c) an est le coefficient de X^n dans Pn. Montrer que an+1 = (n+2)/(n+1) *an
d) Montrer que Pn(-X) = (-1)^n Pn(X)
J'ai fait par récurrence
e) Montrer que P'n+1 = (n+2)Pn
Peut-etre en dérivant et en faisant une récurrence mais je suis alors bloquée par les P''n
f) Montrer que P2n+1(0) = 0 et P2n(0) = (-1)^n
g) Déduire que Pn+1 = Pn+1(0) +(n+2)Integ(Pn(t)dt) [entre 0 et x]
J'ai fait la primitive de P'n+1 et j'ai ajouté Pn+1(0) comme constante
h) Trouver toutes les suites complexes vérifiant Un+2 -2xUn+1 + (1+x²)Un = 0
i) En déduire que Pn = 1/2i * ((X+i)^n+1 - (X-i)^n+1)
Merci d'avance pour votre aide
P0 = 1
Pn+1 = 2XPn- 1/(n+1) * (1+X²)P'n
a) Calculer P1 et P2
P1 = 2X et P2 = 3X²-1
b) Montrer que le degré de Pn est inférieur ou égal à n
J'ai fait une récurrence
c) an est le coefficient de X^n dans Pn. Montrer que an+1 = (n+2)/(n+1) *an
d) Montrer que Pn(-X) = (-1)^n Pn(X)
J'ai fait par récurrence
e) Montrer que P'n+1 = (n+2)Pn
Peut-etre en dérivant et en faisant une récurrence mais je suis alors bloquée par les P''n
f) Montrer que P2n+1(0) = 0 et P2n(0) = (-1)^n
g) Déduire que Pn+1 = Pn+1(0) +(n+2)Integ(Pn(t)dt) [entre 0 et x]
J'ai fait la primitive de P'n+1 et j'ai ajouté Pn+1(0) comme constante
h) Trouver toutes les suites complexes vérifiant Un+2 -2xUn+1 + (1+x²)Un = 0
i) En déduire que Pn = 1/2i * ((X+i)^n+1 - (X-i)^n+1)
Merci d'avance pour votre aide
Re: Suite de polynôme
Salut,
Normalement, par récurrence, je pense que ça devrait marcher sans souci :
Tu suppose que, pour un entier donné, on a
donné, on a 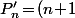P_{n-1}) puis tu utilise la définition (récursive) de
puis tu utilise la définition (récursive) de 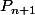 pour évaluer
pour évaluer 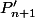 .
.
Certes, dans cette évaluation, il va apparaître du , sauf que ton hypothèse de réccurence implique que
, sauf que ton hypothèse de réccurence implique que 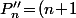P'_{n-1}) et ça devrait faire marcher le truc.
et ça devrait faire marcher le truc.
Sinon, tout le reste semble O.K. sauf ça :
Et sinon, la question h) est mal formulée et n'a pas de sens telle qu'elle est posée vu qu'on y parle d'un certain "x" qui n'a nulle part été défini. Il faut la faire précéder de "Soit x un réel fixé" (ou éventuellement "Soit x un complexe fixé", mais ça complique un peu et c'est inutile). Bref, pour fixer les idées, tu peut prendre par exemple x=3 et regarder si dans ce cas tu sait répondre à la question.
Normalement, par récurrence, je pense que ça devrait marcher sans souci :
Tu suppose que, pour un entier
Certes, dans cette évaluation, il va apparaître du
Sinon, tout le reste semble O.K. sauf ça :
Attention à l'erreur (on ne peut plus grave) consistant à parler de la primitive d'une fonction.c1m2l3e a écrit:g) . . .
J'ai fait la primitive de . . .
Et sinon, la question h) est mal formulée et n'a pas de sens telle qu'elle est posée vu qu'on y parle d'un certain "x" qui n'a nulle part été défini. Il faut la faire précéder de "Soit x un réel fixé" (ou éventuellement "Soit x un complexe fixé", mais ça complique un peu et c'est inutile). Bref, pour fixer les idées, tu peut prendre par exemple x=3 et regarder si dans ce cas tu sait répondre à la question.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Suite de polynôme
D'accord je vais essayer comme ça pour la e)
Pardon pour la g), je n'ai pas fait attention en écrivant
Pour la h), j'ai oublié de marquer que x appartient à R et n appartient à N
Pouvez vous me donner une indication pour la c) si vous en avez une s'il vous plait?
Pardon pour la g), je n'ai pas fait attention en écrivant
Pour la h), j'ai oublié de marquer que x appartient à R et n appartient à N
Pouvez vous me donner une indication pour la c) si vous en avez une s'il vous plait?
Re: Suite de polynôme
Pour la h), le coté "énoncé pas très bien fait", c'est pas super important. Ce que je voulais que tu comprenne bien, c'est que le x est fixé donc que si tu sait comment procéder avec par exemple x=3, tu as quasi répondu à la question.
Pour la c), désolé, j'avais pas fait gaffe que tu avais pas répondu.
Mais d'un autre coté, c'est bébète : tu écrit juste que=a_nX^n+\cdots) en précisant que les points de suspension "contiennent" tout les termes de degré <n et tu regarde ce que ça donne si tu injecte ça dans la définition de
en précisant que les points de suspension "contiennent" tout les termes de degré <n et tu regarde ce que ça donne si tu injecte ça dans la définition de 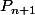 : ça te donne le résultat de façon quasi immédiate.
: ça te donne le résultat de façon quasi immédiate.
Pour la c), désolé, j'avais pas fait gaffe que tu avais pas répondu.
Mais d'un autre coté, c'est bébète : tu écrit juste que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Suite de polynôme
Pour la c) je comprends pas comment faire apparaître le n+2
Pour la e), en faisant comme vous avez dit j'ai un P'n-1 que je ne sais pas par quoi remplacer...
Pour la h) j'ai trouvé les solutions de l'équation caractéristique mais je n'arrive pas à écrire la suite
Pour la e), en faisant comme vous avez dit j'ai un P'n-1 que je ne sais pas par quoi remplacer...
Pour la h) j'ai trouvé les solutions de l'équation caractéristique mais je n'arrive pas à écrire la suite
Re: Suite de polynôme
Si =a_nX^n+\cdots) alors :
alors :
(1)=2a_nX^{n+1}+\cdots) (car les termes de degré <n, une fois multiplié par
(car les termes de degré <n, une fois multiplié par  sont de degré <n+1)
sont de degré <n+1)
(2)=na_nX^{n-1}+\cdots) (car les termes de degré <n ont des dérivés de degré <n-1)
(car les termes de degré <n ont des dérivés de degré <n-1)
(3) (car ...)
(car ...)
donc-\dfrac{1+X^2}{n+1}P'_n(X)=\,?+\cdots)
Pour le (h), une suite géométrique (non identiquement nulle) de raison vérifie
vérifie U_n = 0\ (*))
si et seulement si=0) , c'est à dire
, c'est à dire  (évidement distincts)
(évidement distincts)
Donc les suites géométriques solutions de (*) sont^n\Big)_{n\geq 0}) et
et ^n\Big)_{n\geq 0}) et les suites (pas forcément géométriques) solution de (*) sont les combinaisons linéaires de ces deux suites là (car l'ensemble des solutions est un e.v. de dim. 2 et que les deux suites en question forment une famille libre).
et les suites (pas forcément géométriques) solution de (*) sont les combinaisons linéaires de ces deux suites là (car l'ensemble des solutions est un e.v. de dim. 2 et que les deux suites en question forment une famille libre).
En résumé, les suites vérifiant (*) sont celles telles que^n+\beta (x-i)^n) où
où  et
et  sont deux constantes complexes.
sont deux constantes complexes.
(1)
(2)
(3)
donc
Pour le (h), une suite géométrique (non identiquement nulle) de raison
si et seulement si
Donc les suites géométriques solutions de (*) sont
En résumé, les suites vérifiant (*) sont celles telles que
Modifié en dernier par Ben314 le 22 Aoû 2018, 08:33, modifié 4 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Suite de polynôme
Pour la e) :
(1) Tu dérive la relation définissant (par récurrence)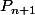 . Le résultat "contient" du
. Le résultat "contient" du  , du
, du 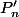 et du
et du  .
.
(2) Par hypothèse de récurrence tu as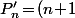P_{n-1}) et donc
et donc 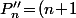P'_{n-1}) et si tu utilise ça dans le résultat du (1) tu obtient un truc qui "contient" maintenant du
et si tu utilise ça dans le résultat du (1) tu obtient un truc qui "contient" maintenant du  , du
, du 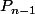 et du
et du  .
.
(3) Sauf que, si tu regarde les termes "contenant" du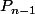 et du
et du  (et que tu t'es pas gouré dans les calculs) ça va forcément (*) être, à un facteur multiplicatif prés, du
(et que tu t'es pas gouré dans les calculs) ça va forcément (*) être, à un facteur multiplicatif prés, du  qui, par définition (de
qui, par définition (de  ) est égal à
) est égal à  .
.
(*) Si un tel "miracle" n'était pas, alors il n'existerais pas de formule telle que celle qu'on te demande de montrer.
(1) Tu dérive la relation définissant (par récurrence)
(2) Par hypothèse de récurrence tu as
(3) Sauf que, si tu regarde les termes "contenant" du
(*) Si un tel "miracle" n'était pas, alors il n'existerais pas de formule telle que celle qu'on te demande de montrer.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Suite de polynôme
J'ai ça du coup,
 - (1+X^2 )P'_{n-1})
mais je vois pas comment faire après parce que si je factorise par (n-2), il ne me semble pas que ça va donner
mais je vois pas comment faire après parce que si je factorise par (n-2), il ne me semble pas que ça va donner
Re: Suite de polynôme
On va dire que c'est "presque bon" et ça ne peut être du qu'à une erreur de calcul à un moment donné.
A priori tu devrait trouver
P'_{n-1}) (et pas
(et pas }XP_{n-1}- (1+X^2 )P'_{n-1}) ).
).
Ce qui donnerais= 2P_n + nP_n=(n\!+\!2)P_n) .
.
Vérifie de nouveau tes calculs et, si tu trouve pas l'erreur, je les ferais de mon coté.
A priori tu devrait trouver
Ce qui donnerais
Vérifie de nouveau tes calculs et, si tu trouve pas l'erreur, je les ferais de mon coté.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Suite de polynôme
D'un autre coté, c'est pas super long donc je peut te le faire :
On suppose que, pour un certain entier , on a
, on a 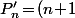P_{n-1}) (et donc
(et donc 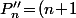P'_{n-1}) ). On a alors :
). On a alors :
-\Bigg(\dfrac{2X}{n\!+\!1}P'_n+\dfrac{1\!+\!X^2}{n\!+\!1}P''_n\Bigg)\cr<br />\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ <br />\Rightarrow\ \ P'_{n+1}=2P_n+\dfrac{2nX}{n\!+\!1}P'_n-\dfrac{1\!+\!X^2}{n\!+\!1}P''_n\ \text{ car }1\!-\!\dfrac{1}{n+1}\!=\!\dfrac{n}{n+1}\cr\cr<br />\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ <br />\Rightarrow\ \ P'_{n+1}=2P_n+2nXP_{n-1}-(1\!+\!X^2)P'_{n-1}\ \text{ grace \`a l'H.R.}\cr\cr<br />\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ <br />\Rightarrow\ \ P'_{n+1}=2P_n+n\Big(2XP_{n-1}-\dfrac{1\!+\!X^2}{n}P'_{n-1}\Big)\cr\cr\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ <br />\Rightarrow\ \ P'_{n+1}=2P_n+nP_n=(n\!+\!2)P_n\ \text{ car, par d\'efinition,} P_n\!=\!2XP_{n-1}-\dfrac{1\!+\!X^2}{n}P'_{n-1})
On suppose que, pour un certain entier
Modifié en dernier par Ben314 le 10 Déc 2018, 06:39, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Suite de polynôme
D'accord merci, j'ai recommencé le calcul et j'ai trouvé la bonne chose.
Pour la question f), est-ce possible en écrivant l'expression de P2n+1 et de P2n à partir de celle de Pn+1? j'ai essayé mais je n'aboutis pas de cette manière, donc je ne sais pas si c'est la bonne
Pour la question f), est-ce possible en écrivant l'expression de P2n+1 et de P2n à partir de celle de Pn+1? j'ai essayé mais je n'aboutis pas de cette manière, donc je ne sais pas si c'est la bonne
Re: Suite de polynôme
Oui, c'est ça, mais tu peut même uniquement regarder ce que donne la définition (récursive) de 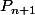 dans le cas où on prend
dans le cas où on prend 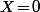 .
.
Tu regardera (et/ou comprendra) ensuite pourquoi il est nécessaire de distinguer le cas pair du cas
pair du cas  impair.
impair.
Indic : Tu va aussi avoir besoin du résultat de la question e) pour te "débarrasser" du)
Tu regardera (et/ou comprendra) ensuite pourquoi il est nécessaire de distinguer le cas
Indic : Tu va aussi avoir besoin du résultat de la question e) pour te "débarrasser" du
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Suite de polynôme
Je trouve
= -1/(2n+1) * P'_{2n})
et
= -1/(2n) * P'_{2n-1})
Après je ne vois pas comment utiliser la question d'avant, on aurait
P_{2n-1}) et
et

Mais je ne vois pas comment le fait de les insérer dans les autres équations donneraient le résultat souhaité
et
Après je ne vois pas comment utiliser la question d'avant, on aurait
Mais je ne vois pas comment le fait de les insérer dans les autres équations donneraient le résultat souhaité
Re: Suite de polynôme
c1m2l3e a écrit:Je trouve
et
Après je ne vois pas comment utiliser la question d'avant, on auraitet
1) Il te manque les "(0)" dans tes deux trucs (et vu les notations employées, c'est évidement on ne peut plus important)
2) Si
Idem pour l'autre.
(et je redit que, jusque là, ça sert à rien de distinguer le cas
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Suite de polynôme
Non, il y a encore une erreur de calcul.
Pour tout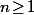 on a :
on a :
(1)=2\!\times\!0\!\times\!P_n(0)-\dfrac{1\!+\!0^2}{n\!+\!1}P'_n(0)=-\dfrac{1}{n\!+\!1}P'_n(0))
(2)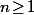 on a
on a 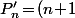P_{n-1}\ \ \Rightarrow\ \ P'_n(0)\!=\!(n\!+\!1)P_{n-1}(0))
Donc=-P_{n-1}(0)) pour tout
pour tout 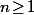
Ce qui signifie que=-P_{n-2}(0)=+P_{n-4}(0)=-P_{n-6}(0)=+P_{n-8}(0)=\cdots) et à force de diminuer de 2 en 2, on va tomber au final soit sur
et à force de diminuer de 2 en 2, on va tomber au final soit sur ) si le
si le  de départ est impair, soit sur
de départ est impair, soit sur ) si le
si le  de départ est pair.
de départ est pair.
Pour tout
(1)
(2)
Donc
Ce qui signifie que
Modifié en dernier par Ben314 le 21 Aoû 2018, 19:41, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Suite de polynôme
Oui je suis d'accord mais je ne comprends pas comment on peut en déduire les égalités demandées... Parce que  =1 = (-1)^0) donc c'est vérifié pour n=0 mais ça veut pas dire que c'est valable pour tous les n, si?
donc c'est vérifié pour n=0 mais ça veut pas dire que c'est valable pour tous les n, si?
Re: Suite de polynôme
Ca "ne veut pas dire" que ça va tout le temps être vrai, mais pour le prouver, c'est on ne peut plus simple partant de la relation \!=\!-P_{n-2}(0)) :
:
Soit tu fait comme dans le post juste au dessus avec des points de suspension et tu "compte" combien d'étapes il y a pour savoir si à la fin on tombe sur du\!=\!+1) ou bien sur du
ou bien sur du \!=\!-1) , soit tu trouve que c'est pas assez "propre" comme preuve et tu fait une récurrence.
, soit tu trouve que c'est pas assez "propre" comme preuve et tu fait une récurrence.
C'est bien évidement deux fois la même chose rédigé de façon un peu différente : la récurrence fait "plus propre", mais perso, je trouve que l'autre méthode est bien plus naturelle vu que, contrairement à la récurrence, elle ne fait pas que prouver que le résultat est valable, mais elle explique aussi d'où il provient.
Soit tu fait comme dans le post juste au dessus avec des points de suspension et tu "compte" combien d'étapes il y a pour savoir si à la fin on tombe sur du
C'est bien évidement deux fois la même chose rédigé de façon un peu différente : la récurrence fait "plus propre", mais perso, je trouve que l'autre méthode est bien plus naturelle vu que, contrairement à la récurrence, elle ne fait pas que prouver que le résultat est valable, mais elle explique aussi d'où il provient.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
23 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
