Suite numérique

[Skullkid]

Bonjour, je bute sur l'exo suivant :

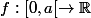
Soient a > 0 et une fonction telle que . Montrer que .

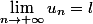
J'écris donc mais après je bloque. Comme c'est censé être un exo sur les suites, j'ai posé et je veux montrer que . J'ai essayé divers trucs dont le passage au ln mais sans grand succès. Peut-être suis-je sur la mauvaise voie ?

Merci d'avance à ceux qui pourront m'aider.

[Pythales]

et d'après Cesaro, cette dernière somme tend vers

[ThSQ]

Ton énoncé doit manqer des trucs car que vaut f(a) ? et j'imagine que f(x) > 0.

Sinon prends le log + Césaro.



Edit : grillé par Pythales ;)

[Skullkid]

Oui, c'est pas précisé mais je suppose que tout est strictement positif. Merci à vous deux, je dois dire que j'aurais jamais pensé à Césaro...