Suite d'intégrales
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
spe20051
- Membre Naturel
- Messages: 13
- Enregistré le: 26 Mai 2019, 11:09
-
 par spe20051 » 26 Mai 2019, 11:18
par spe20051 » 26 Mai 2019, 11:18
Bonjour,
auriez-vous des idées pour calculer cette limite ?
}{1+nt}dt})
où f est continue dans [0,1]
J'ai essayé d'encadrer f mais ou ne connait pas son signe...et par intégration par parties ça ne marche pas non plus.
-
aviateur
 par aviateur » 26 Mai 2019, 11:36
par aviateur » 26 Mai 2019, 11:36
Bonjour
Tu majores la valeur absolue et tu peux sortir alors

il te reste une intégrale facile à calculer qui tend vers 0.
Ou sinon tu appliques le th de CV dominée.
-
spe20051
- Membre Naturel
- Messages: 13
- Enregistré le: 26 Mai 2019, 11:09
-
 par spe20051 » 26 Mai 2019, 11:59
par spe20051 » 26 Mai 2019, 11:59
Bonjour,
merci pour la réponse, mais je n’ai pas vu en cours le théorème de convergence dominée et ||f||. N’y a t’il pas plus simple comme méthode ?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Mai 2019, 12:38
par GaBuZoMeu » 26 Mai 2019, 12:38
Fixons
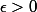
.
Choisir

tel que
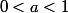
et que, pour tout entier naturel

,
}{1+nt}\,dt\right|<\frac{\epsilon}2})
.
Choisir ensuite

tel que, pour tout
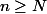
,
}{1+nt}\,dt\right|<\frac{\epsilon}2)
.
-
spe20051
- Membre Naturel
- Messages: 13
- Enregistré le: 26 Mai 2019, 11:09
-
 par spe20051 » 26 Mai 2019, 13:12
par spe20051 » 26 Mai 2019, 13:12
Merci, mais comment je choisis a étant donné que je n’ai aucune information sur f ?
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 26 Mai 2019, 13:12
par LB2 » 26 Mai 2019, 13:12
f est continue sur un segment donc bornée
-
spe20051
- Membre Naturel
- Messages: 13
- Enregistré le: 26 Mai 2019, 11:09
-
 par spe20051 » 26 Mai 2019, 13:16
par spe20051 » 26 Mai 2019, 13:16
Euh oui mais je ne vois pas quelle valeur choisir pour a, pouvez-vous m'expliquez ?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Mai 2019, 13:40
par GaBuZoMeu » 26 Mai 2019, 13:40
Tout de même, ne peux-tu pas majorer
}{1+nt}\,dt\right|)
en fonction de

et de
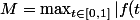|)
, indépendamment de

?
-
spe20051
- Membre Naturel
- Messages: 13
- Enregistré le: 26 Mai 2019, 11:09
-
 par spe20051 » 26 Mai 2019, 15:53
par spe20051 » 26 Mai 2019, 15:53
Bah,
}{1+nt}}dt \right|\leq a\max_{t\in [0,1]}\left|f(t)\right|)
?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Mai 2019, 15:58
par GaBuZoMeu » 26 Mai 2019, 15:58
Alors maintenant, vois-tu quelle valeur choisir pour

?
-
spe20051
- Membre Naturel
- Messages: 13
- Enregistré le: 26 Mai 2019, 11:09
-
 par spe20051 » 26 Mai 2019, 16:03
par spe20051 » 26 Mai 2019, 16:03
Si a=1/2
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 26 Mai 2019, 16:09
par LB2 » 26 Mai 2019, 16:09
a va dépendre de f
-
spe20051
- Membre Naturel
- Messages: 13
- Enregistré le: 26 Mai 2019, 11:09
-
 par spe20051 » 26 Mai 2019, 16:13
par spe20051 » 26 Mai 2019, 16:13
Ok mais je ne vois vraiment pas quelle valeur choisir dans ce cas
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Mai 2019, 16:13
par GaBuZoMeu » 26 Mai 2019, 16:13
M'enfin ???
Posons
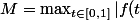|)
.
Est-ce si difficile que ça de choisir

tel que

?
-
spe20051
- Membre Naturel
- Messages: 13
- Enregistré le: 26 Mai 2019, 11:09
-
 par spe20051 » 26 Mai 2019, 16:20
par spe20051 » 26 Mai 2019, 16:20
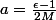
?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Mai 2019, 20:56
par GaBuZoMeu » 26 Mai 2019, 20:56
Perdu !

a vocation à être très petit. Donc

n'est sûrement pas une bonne idée, il a toutes chances d'être négatif :
-
spe20051
- Membre Naturel
- Messages: 13
- Enregistré le: 26 Mai 2019, 11:09
-
 par spe20051 » 26 Mai 2019, 21:06
par spe20051 » 26 Mai 2019, 21:06

?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Mai 2019, 21:08
par GaBuZoMeu » 26 Mai 2019, 21:08
Oui, ça c'est nettement mieux !
-
spe20051
- Membre Naturel
- Messages: 13
- Enregistré le: 26 Mai 2019, 11:09
-
 par spe20051 » 26 Mai 2019, 21:10
par spe20051 » 26 Mai 2019, 21:10
Et donc après, il va falloir que je fasse pareil pour l'autre partie de l'intégrale ?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Mai 2019, 21:52
par GaBuZoMeu » 26 Mai 2019, 21:52
Oui, une fois que

est fixé on peut majorer à la louche la valeur absolue du deuxième morceau (avec une majoration dépendant de

cette fois-ci) pour montrer que c'est plus petit que
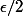
pour

suffisamment grand.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités