Suite d'intégrales
28 messages
- Page 2 sur 2 - 1, 2
Re: Suite d'intégrales
Je comprend pas le "majorer à la louche", je dois prendre quoi comme majorant ?
Re: Suite d'intégrales
à la louche, ça veut dire majorer }{1+nt}\, dt\right|) sans finasser, mais en gardant présent à l'esprit le but : montrer qu'on peut rendre ça plus petit que
sans finasser, mais en gardant présent à l'esprit le but : montrer qu'on peut rendre ça plus petit que 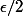 en prenant
en prenant  suffisamment grand.
suffisamment grand.
Rappel : on a pris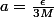 , où
, où 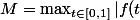|) .
.
Rappel : on a pris
Re: Suite d'intégrales
OK, déjà est ce que je peux majorer comme j'avais fait avant par (1-a)sup(f) ?
Re: Suite d'intégrales
Tu peux mais ça ne va pas t'avancer à grand chose puisque ça ne dépend pas de n !
Je te laisse te débrouiller, moi je me couche.
Je te laisse te débrouiller, moi je me couche.
Re: Suite d'intégrales
(1-a)sup(f) a de grandes chances d'être négatif
si tu trace quelques fonction 1/(1+nx), tu t’aperçoit que
-> coté droite, la fonction tend vers 0, donc si on multiple ça par une fonction borné, le tout tend vers 0, donc l'intégrale aussi.
-> coté gauche : on tend vers 1, et il y a concurrence entre n et la borne de séparation choisi.
par continuité de f en 0 (existence d'un majorant de |f|), sur [0;a], on va majorer la valeur de l'intégrale en prenant a petit.
par limite de 1/(1+nx), sur [a;1], on va augmenter n pour faire tendre l'intégrale vers 0.
Il faut absolument que que a soit indépendant de n, sinon on ne peut pas encadrer la partie de droite une fois que celle de gauche est faite.
Comme on ne sait pas où se trouve a, majorer |f| sur [0;1] entier et pas sur [0;a] permet d'avoir une définition du majorant utilisé. On aurait pu majorer f sur [0;0000000000000.1] et travailler avec la condition a < 0000000000000.1.
NB : que f soit bornée et intégrable suffirait, f continue en 0 et intégrale est peut être suffisant
si tu trace quelques fonction 1/(1+nx), tu t’aperçoit que
-> coté droite, la fonction tend vers 0, donc si on multiple ça par une fonction borné, le tout tend vers 0, donc l'intégrale aussi.
-> coté gauche : on tend vers 1, et il y a concurrence entre n et la borne de séparation choisi.
par continuité de f en 0 (existence d'un majorant de |f|), sur [0;a], on va majorer la valeur de l'intégrale en prenant a petit.
par limite de 1/(1+nx), sur [a;1], on va augmenter n pour faire tendre l'intégrale vers 0.
Il faut absolument que que a soit indépendant de n, sinon on ne peut pas encadrer la partie de droite une fois que celle de gauche est faite.
Comme on ne sait pas où se trouve a, majorer |f| sur [0;1] entier et pas sur [0;a] permet d'avoir une définition du majorant utilisé. On aurait pu majorer f sur [0;0000000000000.1] et travailler avec la condition a < 0000000000000.1.
NB : que f soit bornée et intégrable suffirait, f continue en 0 et intégrale est peut être suffisant
Re: Suite d'intégrales
(1-a)sup(f) a de grandes chances d'être négatif
c'est bien sûr
28 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
