Bonjour.
je suis bloquée sur un exercice sur des suites si vous pouviez m'aider pour que je puisse continuer ensuite.
on considère la suite Pn(x)=1 + x + x² + ... + x^(2n-1) + x^(2n)
Po(x)=1, P1(x)=1 + x + x², P2(x)=1 + x + x² + x^3 + x^4
pour tout x différent de 1 Pn(x)= (1-x^(2n+1))/(1-x)
pour tout n dans IN, on pose bn=inf(Pn(x)) dans IR
> montrer que pour n positif, il existe un réel unique an pour lequel
bn=Pn(an) on posera ao=0
> montrer que la suite (an) admet un limite alpha que l'on determinera
si vous pouviez m'aider ce serait sympa, sinon c'est pas grave.
Minacristal
PS: les n sont en indice
Suite de fonctions polynomiales
2 messages
- Page 1 sur 1
Bonjour,
déjà tu peux remarquer que pour> 1) et
et =1) donc
donc  est atteint sur
est atteint sur  .
.
ensuite posons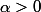 ,
, =\frac{1+\alpha^{2n+1}}{1+\alpha}\geq 1) si
si 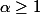 , donc
, donc  est atteint sur
est atteint sur 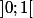 .
.
Reste à trouver le min de=\frac{x^{2n+1}+1}{x+1}) sur
sur  .
.
On sait qu'il est atteint car [0;1] est compact et une étude de fonction nous apprend que est décroissante sur
est décroissante sur  puis croissante sur
puis croissante sur  , ce qui prouve l'unicité de
, ce qui prouve l'unicité de  .
.
Reste à trouver ou alors à minorer ou majorer
ou alors à minorer ou majorer  ...
...
 est le nombre de [0;1] où la dérivée de
est le nombre de [0;1] où la dérivée de  s'annule et donc
s'annule et donc x^2n-1=0)
Je te conseille par exemple de minorer par
par )
déjà tu peux remarquer que pour
ensuite posons
Reste à trouver le min de
On sait qu'il est atteint car [0;1] est compact et une étude de fonction nous apprend que
Reste à trouver
Je te conseille par exemple de minorer
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
