Suite en fonction d'un paramètre

[carpediem69]

[FONT=Comic Sans MS]Bonjour, je voulais une indication. Je suis en train de lire une correction de problème faite par mon prof et je ne comprends pas une de ses affirmations. Il dit que la suite (n*a^n) où n est un entier naturel et a un complexe converge si et seulement si le module de a est strictement inférieur à 1.

Cela semble évident dans sa correction mais je n'arrive pas à le démontrer. Plus précisément j'arrive à montrer que la suite diverge si le module de a est supérieur ou égal à 1. Mais le cas de convergence reste pour moi un mystère (bien que le question semble élémentaire).

Une petite aide de votre part serait la bienvenue. Sur ce, je vous souhaite une excellente journée et un grand merci aux personnes qui dévoueront quelques minutes de leur précieuse journée pour me venir en aide. =)[/FONT]

[Bony]

Le truc à savoir c'est qu'une fonction en a^n c'est comme une exponentielle ça croit très vite si a > 1 et décroit très vite si a < 1 par rapport à n.

Tu peux écrire n*a^n = n*exp(n*ln(a)) et comme a < 1 ln(a) < 0 donc exp(n*ln(a)) -> 0 lorsque n -> +infini

[girdav]

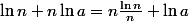et on peut écrire que . Pour assez grand, est plus petit que , donc .

[carpediem69]

Merci pour vos réponses ! Toutefois a est un complexe et on ne peut pas prendre le logarithme d'un nombre complexe (à mon niveau en tout cas), n'est ce pas ?

[carpediem69]

Ou sinon on peut contourner cette difficulté du ln(a) avec a un complexe en passant à la notation exponentielle. n*r^n*exp(i*n*theta). On passe au module et on est ramené au cas réel avec n*r^n. et la suite des modules tendra vers zéro, la suite complexe tendra vers 0 également.

[girdav]

Merci pour vos réponses ! Toutefois a est un complexe et on ne peut pas prendre le logarithme d'un nombre complexe (à mon niveau en tout cas), n'est ce pas ?

Tu peux toujours te ramener au cas où est réel en prenant le module.

[arnaud32]

si |a|1 tu as |a^n|=|a|^n et comme on te l'a montre ca tend vers +oo donc la suite diverge

si |a|=1 tu as qui converge ssi t=0[2\pi]