Bonjour à tous,
je regarde le première exemple du 4) Développements asymptotiques
de ce cours: http://mp.cpgedupuydelome.fr/cours.php? ... rtie=78505
Je ne comprends pas le passage du milieu à l'égalité de droite:
fn(Xn+1)=X^{n}_{n+1} − X_{n+1}−1 = X^n_{n+1} − X^{n+1}_{n+1}<0
"et donc x^{n+1}<x^n."
La suite est décroissante... etc
Merci d'avance
Suite développement asymptotique
5 messages
- Page 1 sur 1
Re: Suite développement asymptotique
Salut,
Vu que est strictement croissante et que
est strictement croissante et que \!=\!0) , c'est que
, c'est que 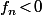 sur [1,x_n[[/tex] et est
sur [1,x_n[[/tex] et est 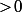 sur
sur 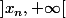 .
.
Donc le fait que\!<\!0) montre que
montre que 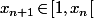 .
.
Vu que
Donc le fait que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Suite développement asymptotique
Ben314 a écrit:Salut,
Vu queest strictement croissante et que
, c'est que
sur [1,x_n[[/tex] et est
sur
.
Donc le fait quemontre que
.
Merci Ben,
en fait ce que je n'arrive pas à retrouver c'est le passage après la deuxième égalité, où est passé le -1? Et pourquoi X_{n+1} devient X^{n+1}_{n+1}
Re: Suite développement asymptotique
Parce que, toujours par définition, \!=\!0) c'est à dire
c'est à dire 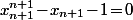 soit encore
soit encore 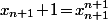 .
.
Ce qu'il faut évidement bien comprendre, c'est que concernant n'importe quel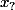 , la seule et unique chose que tu sache (au début), c'est que c'est l'unique solution de
, la seule et unique chose que tu sache (au début), c'est que c'est l'unique solution de \!=\!0) .
.
Donc c'est même pas la peine de se demander d'où "sort" une quelconque égalité concernant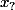 vu que ça ne peut provenir que de là.
vu que ça ne peut provenir que de là.
Ce qu'il faut évidement bien comprendre, c'est que concernant n'importe quel
Donc c'est même pas la peine de se demander d'où "sort" une quelconque égalité concernant
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Suite développement asymptotique
Ben314 a écrit:Parce que, toujours par définition,c'est à dire
soit encore
.
Ce qu'il faut évidement bien comprendre, c'est que concernant n'importe quel, la seule et unique chose que tu sache (au début), c'est que c'est l'unique solution de
.
Donc c'est même pas la peine de se demander d'où "sort" une quelconque égalité concernantvu que ça ne peut provenir que de là.
Merci Ben, ton explication est très claire.
En effet je n'arrivais pas à voir cela.
encore merci!
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
