Suite des solutions d'1 equation

[dilzydils]

Bonsoir

je considere l'équation 1+x+x^2/2+...+x^n/n!-a*exp(x)=0
où a est un reel dans ]0;1[.
Il s'agit de montrer l'existence d'un unique solution sur R+.
L'existence, ca va avec le TVI mais je bloque sur l'unicité.

Merci de votre aide

[Mikou]

1+x+x^2/2+...+x^n/n! tu sais de quelle fonction c'est le dvl limité en serie ?

[dilzydils]

Je sais que c'est la partie réguliere du DL de exp en 0.
A part ca,.??

[nuage]

Salut,
à part ça : dérivation et récurrence.

[dilzydils]

J'avais deja derivé et constaté que si on note f(n):x->1+x+x^2/2+...+x^n/n!-a*exp(x) on a f(n)'=f(n-1)
Mais je m'interroge sur la forme du rst: est-ce de l'analyse synthese, i.e je suppose le probleme resolu et j'en déduis des conditions pour une recurrence>??

[nuage]

Salut,
il reste à étudier les variations de

[yos]

Hypothèse de récurrence : fn possède une racine unique a sur R+.
Puisque fn(0)>0 et limfn=-oo (en +oo).
Tu as le signe de fn : positive sur [O,a] et négative sur [a,+oo[.
Tu as donc les variations de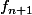 : croissante sur [O,a] et décroissante sur [a,+oo[. De plus , donc 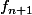est strictement positive sur [0,a]. Sur [a, +oo[, 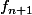est décroissante et change de signe d'où une racine unique pour .
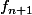Cela achève la récurrence. En plus tu as le fait que la suite a(n) des racines est croissante.