Suite définie par une relation de récurrence

[math71]

Bonjour,
Soit (a) et (b) deux suites de réels positifs convergent respectivement vers a et 0. On suppose que a<1.
On définit la suite u par: u 0 et u = au+b.
Montrer que u tend vers 0.
J'ai traduit avec des epsilon que a et b convergent vers a et 0.
J'ai montré que u est une suite positive et que à partir d'un certain rang a est inférieur à 1.
mais je ne vois plus quoi faire...
Merci pour un petit coup de pouce!

[Ben314]

Salut,
On peut s'en sortir avec une "simple" comparaison avec des suites arithmético-géométrique :
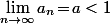
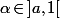
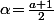
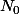
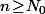
- Comme , si on fixe un (par exemple ), on sait qu'il existe un entier tel que, pour tout , on ait .
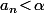
- On choisi maintenant un .
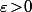
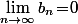
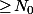
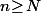
Comme , il existe un entier , qu'on peut choisir , tel que, pour tout , on ait .
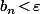
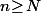
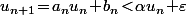
Pour tout , on a donc c'est à dire et on a donc (récurrence évidente) pour tout .
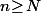
(c'est ici qu'il faut connaître les suites arithmético géométriques et la façon dont on les manipule)
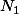
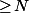
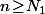
Comme il existe un entier il existe un entier qu'on peut choisir tel que, pour tout , on ait ce qui signifie que
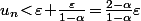
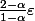
Et comme peut être choisi arbitrairement petit (en choisissant assez petit et en n'oubliant pas que le est une simple constante) cela prouve bien que

[math71]

Encore merci! Je viens de me rendre compte que c'est toujours vous qui m'expliquez les solutions, encore merci et bonne soirée.