Suite convergente
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nicolas2
- Membre Naturel
- Messages: 67
- Enregistré le: 30 Déc 2011, 16:36
-
 par nicolas2 » 16 Mar 2015, 19:21
par nicolas2 » 16 Mar 2015, 19:21
Bonjour,
je dois démontrer que cette suite converge Un=
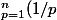 - ln(n))
Or je ne sais pas vraiment par où commencer ..
Merci d'avance

-
mathelot
 par mathelot » 16 Mar 2015, 19:25
par mathelot » 16 Mar 2015, 19:25
tu peux comparer
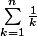
à une intégrale

et
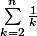
ça fait comme des sommes de Darboux pour l'intégrale de Riemann.
tu peux tracer l'hyperbole d'équation xy=1 et dessiner des rectangles de hauteur
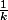
et de base 1
-
nicolas2
- Membre Naturel
- Messages: 67
- Enregistré le: 30 Déc 2011, 16:36
-
 par nicolas2 » 16 Mar 2015, 19:28
par nicolas2 » 16 Mar 2015, 19:28
Je n'ai encore ni étudié les intégrales, ni étudié les sommes de Darboux .. :/

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 16 Mar 2015, 19:56
par zygomatique » 16 Mar 2015, 19:56
salut
dans le supérieur ? ... et tu ne connais pas les intégrales ? ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
nicolas2
- Membre Naturel
- Messages: 67
- Enregistré le: 30 Déc 2011, 16:36
-
 par nicolas2 » 16 Mar 2015, 20:01
par nicolas2 » 16 Mar 2015, 20:01
Oui en ECE.
Je connais les intégrales mais je ne les ai pas encore étudiés cette année, donc je ne pense devoir résoudre cet exercice avec ....

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 16 Mar 2015, 20:09
par zygomatique » 16 Mar 2015, 20:09
très difficile alors ....
et qu'as-tu étudié alors ? ... qu'on puisse savoir quoi utiliser .... mais bon ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 16 Mar 2015, 20:22
par Joker62 » 16 Mar 2015, 20:22
Hello,
-u(n) = \dfrac{1}{n+1} + \ln\left(\dfrac{n}{n+1}\right) = \dfrac{1}{n+1} + \ln\left(1-\dfrac{1}{n+1}\right) \le 0)
(u_n) est donc décroissante.
Minorée peut-être ? (Après faut voir ce que t'as comme connaissances en effet)
-
nicolas2
- Membre Naturel
- Messages: 67
- Enregistré le: 30 Déc 2011, 16:36
-
 par nicolas2 » 16 Mar 2015, 20:39
par nicolas2 » 16 Mar 2015, 20:39
On va dire que c'est dans le cadre de révisions pour un DS sur limite, monotonie, continuité et dérivation ..
Peut-être faut-il utiliser le théorème de la limite monotone, mais j'ai du mal à voir son application ici .. mais je crois que le prof à donner ça comme indication. En précisant bien qu'on ne cherche pas la limite ou le maximum/minimum, mais simplement à démontrer que la suite converge.
Et sa limite est appelée constante d'Euler ..

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 16 Mar 2015, 20:47
par zygomatique » 16 Mar 2015, 20:47
oui la suite est décroissante ... et minorée par 0 ....
mais pour montrer ce dernier point c'est pas évident à priori ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
nicolas2
- Membre Naturel
- Messages: 67
- Enregistré le: 30 Déc 2011, 16:36
-
 par nicolas2 » 16 Mar 2015, 20:53
par nicolas2 » 16 Mar 2015, 20:53
On a fait cet exemple en cours que je viens de retrouver .. Il faut à priori s'en servir
On a démontré que pour tout n supérieur ou égale à 2 :
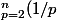 < ln(n) < \bigsum_{p=1}^{n-1} (1/p))
-
mathelot
 par mathelot » 16 Mar 2015, 20:56
par mathelot » 16 Mar 2015, 20:56
en tous cas
 \leq 1+\frac{1}{2}+..+\frac{1}{n} -ln(n))
en comparant suite et intégrale.

-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 16 Mar 2015, 21:15
par Pythales » 16 Mar 2015, 21:15
Joker62 a écrit:Hello,
-u(n) = \dfrac{1}{n+1} + \ln\left(\dfrac{n}{n+1}\right) = \dfrac{1}{n+1} + \ln\left(1-\dfrac{1}{n+1}\right) \le 0)
(u_n) est donc décroissante.
Minorée peut-être ? (Après faut voir ce que t'as comme connaissances en effet)
La série
^2})
est convergente, de même que la suite

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités