Suite bornée

par **Anonyme** » 02 Nov 2005, 18:04

Bonjour
Est ce qu' on peut dire que: si Un est non bornée alors sa valeur absolue est supérieure à n.
Et merci d'avance

par **Zebulon** » 02 Nov 2005, 18:12

Bonsoir,
soit pour tout n entier,

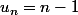
. Alors

n'est pas bornée et [TEX]u_n0. Donc non, on ne peut pas dire ça...
Zeb.

par **Anonyme** » 02 Nov 2005, 18:36

Merci d'abord
Soit K un intervalle non borné est ce qu'il existe forcément une suite d'élément de K telle que sa valeur absolue est supérrieure à n

par **Zebulon** » 02 Nov 2005, 18:47

Cette fois, l'énoncé est trop vague:est-ce un intervalle de lR? Le n est-il le même que l'indice de la suite?

par **Anonyme** » 02 Nov 2005, 19:36

excuse moi je doit vraiment préciser
K appartient à R et n est l'indice de la suite

par **Zebulon** » 02 Nov 2005, 20:19

Là, selon moi, c'est même pire qu'avant! Tu peux prendre une suite constante

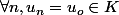
et pour n assez grand, n est supérieur

.
Zeb.

par **Anonyme** » 02 Nov 2005, 23:29

Excuse moi , mais c'est le contraire , je veux trouver une suite Un appartient à K telle que la valeur absolue de Un est SUPERIEURE à n

par **boulay59** » 02 Nov 2005, 23:49

Un intervalle de |R non borné contient nécessairement un intervalle de la forme [a, +oo[. Si tu prends la suite

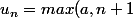, alors sauf erreur, elle convient

par **Anonyme** » 03 Nov 2005, 00:01

on a -l'inf;a ne contient pas forcément b;+l'inf

par **Anonyme** » 03 Nov 2005, 10:14

mais un intervalle e R ne contient pas forcément un intervalle de la forme a;+00 (contre exemple: prenons -00;b )

par **boulay59** » 03 Nov 2005, 13:34

Autant pour moi, j'ai fait l'erreur à ne pas faire : j'ai confondu borné avec majoré.

Mais là, ça a permis une chose : que tu trouves seule la réponse à ta question (je pense qu'avec les intervalles que tu as donnés, tu devrais trouver rapidement un contre-exemple)

Suite bornée

suite bornée

suite bornée

suite bornée

suite bornée

Qui est en ligne