Statistique Moyenne et Variance
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 08 Oct 2013, 19:18
par Dante0 » 08 Oct 2013, 19:18
Bonjour,
Je bloque sur quelques écritures en statistiques.
Pour la variance :
 = V(\frac{1}{n} \bigsum_{i=1}^{n} X_i) = \frac{1}{n^2} \bigsum_{i=1}^{n} V(X_i) = \frac{1}{n^2} \bigsum_{i=1}^{n} \sigma^2 = \frac{n\sigma^2}{n^2} = \frac{\sigma^2}{n})
Deux choses que je ne comprends pas ici : pourquoi on a un n² au dénominateur lorsqu'on "sort" 1/n de la variance à la 2e étape.
Et d'ou vient le n au numérateur à l'avant dernière étape ?
Ensuite pour la moyenne de la variance empirique.
On sait que la variance empirique est
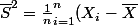)
On veux montrer que la moyenne de la variance empirique est égale à
 = \frac{n-1}{n}\sigma^2)
Voici les étapes :
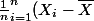^2)
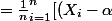-(\bar{X}-\alpha)]^2)
^2 -2(\bar{X}-\alpha)\frac{1}{n} \bigsum_{i=1}^{n}(X_i-\alpha) + (\bar X -\alpha)^2)
^2 -2(\bar X -\alpha)^2 +(\bar X -\alpha)^2)
^2 -(\bar X -\alpha)^2)
D'ou :
 = \frac{1}{n} \bigsum_{i=1}^{n} V(X_i) - V(\bar{X}) = \sigma^2 -\frac{\sigma^2}{n} = \frac{n-1}{n}\sigma^2)
La par contre je suis bloqué dès la première étape... :hein:
Merci !

-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 09 Oct 2013, 16:15
par Dante0 » 09 Oct 2013, 16:15
Up :help: :help:
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 09 Oct 2013, 16:38
par Sylviel » 09 Oct 2013, 16:38
Salut !
pourquoi on a un n² au dénominateur lorsqu'on "sort" 1/n
C'est une propriété de la variance : var(a X) = a²var(X). En effet "la variance est un carré" (reviens à la définition de la variance).
d'ou vient le n au numérateur à l'avant dernière étape
de la somme : tu fais sigma²+sigma²+...+sigma² n fois.
Rq tu ne peux faire Var(X+Y)= Var(X)+Var(Y) que si tu as indépendance.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 09 Oct 2013, 16:48
par Dante0 » 09 Oct 2013, 16:48
Sylviel a écrit:Salut !
C'est une propriété de la variance : var(a X) = a²var(X). En effet "la variance est un carré" (reviens à la définition de la variance).
de la somme : tu fais sigma²+sigma²+...+sigma² n fois.
Rq tu ne peux faire Var(X+Y)= Var(X)+Var(Y) que si tu as indépendance.
Merci!
Me reste plus qu'a comprendre la moyenne empirique maintenant ^^
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 09 Oct 2013, 17:12
par Sylviel » 09 Oct 2013, 17:12
j'imagine que alpha est l'espérance de X_i, non ?
la première ligne (un carré est oublié au début) est juste un jeu d'écriture (tu ajoute et retire alpha).
Ensuite tu développe.
Et à la fin tu prends l'espérance de l'égalité et utilise la définition de la variance :
Var(X)= E(X²)-E(X)²
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 09 Oct 2013, 18:18
par Dante0 » 09 Oct 2013, 18:18
Sylviel a écrit:j'imagine que alpha est l'espérance de X_i, non ?
la première ligne (un carré est oublié au début) est juste un jeu d'écriture (tu ajoute et retire alpha).
Ensuite tu développe.
Et à la fin tu prends l'espérance de l'égalité et utilise la définition de la variance :
Var(X)= E(X²)-E(X)²
On développe comment au juste ici ? Ca ressemble à une identité remarquable mais de loin...
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 09 Oct 2013, 18:19
par Sylviel » 09 Oct 2013, 18:19
oui c'est tout bêtement (A-B)²
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 09 Oct 2013, 21:35
par Dante0 » 09 Oct 2013, 21:35
Sylviel a écrit:oui c'est tout bêtement (A-B)²
D'ou viens la somme alors ? Et le premier terme
^2)
?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 09 Oct 2013, 22:26
par Sylviel » 09 Oct 2013, 22:26
C'est la définition de la variance empirique. Je ne vois pas vraiment ton problème en fait ?
Si tu veux tu peux écrire la suite d'égalité sans la somme et le 1/n (juste de la réécriture), puis tu ajoutes la somme et le 1/n pour obtenir la définition de la variance empirique, puis tu prends l'espérance pour obtenir le résultat.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 10 Oct 2013, 14:20
par Dante0 » 10 Oct 2013, 14:20
Je ne comprends pas comment on passe de
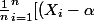-(\bar{X}-\alpha)]^2)
à
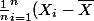^2 -2(\bar{X}-\alpha)\frac{1}{n} \bigsum_{i=1}^{n}(X_i-\alpha) + (\bar X -\alpha)^2)
Si on ne fait que développer grâce à l'identité remarquable, d'ou vient la somme au milieu de la 2e expression ? Ou alors on a brulé des étapes ? Parce que je vois vraiment pas comment on passe de l'un à l'autre
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 10 Oct 2013, 15:06
par Sylviel » 10 Oct 2013, 15:06
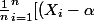-(\bar{X}-\alpha)]^2)
à
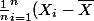^2 -2(\bar{X}-\alpha)\frac{1}{n} \bigsum_{i=1}^{n}(X_i-\alpha) + (\bar X -\alpha)^2)
Je disais donc
-(\bar{X}-\alpha)]^2 =(X_i -\alpha)^2-2(X_i -\alpha)(\bar{X}-\alpha) <br />+ (\bar{X}-\alpha)^2)
je prends la somme
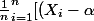-(\bar{X}-\alpha)]^2 <br />=\frac{1}{n}\bigsum_{i=1}^{n} [(X_i -\alpha)^2-2(X_i -\alpha)(\bar{X}-\alpha) <br />+ (\bar{X}-\alpha)^2)
ensuite on distribue
^2]- \frac{1}{n}\bigsum_{i=1}^{n} [2(X_i -\alpha)(\bar{X}-\alpha) ]<br />+\frac{1}{n}\bigsum_{i=1}^{n}[ (\bar{X}-\alpha)^2 ])
Puis on sors les termes constants
^2]<br />- 2(\bar{X}-\alpha) \frac{1}{n}\bigsum_{i=1}^{n} [(X_i -\alpha)]<br />+(\bar{X}-\alpha)^2)
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 11 Oct 2013, 08:25
par Dante0 » 11 Oct 2013, 08:25
Pour le dernier terme tu fais
(x-a)²+(x-a)²+...+(x-a)² avec n termes, donc cela te donne n*(x-a)² que tu divise par n.
Pour le terme du milieu c'est de la factorisation toute simple :
a x1 + a x2 + ... + a xn = a (x1 + x2 + ... + xn)
Edit : sorry danteo j'ai cliquer sur modifier au lieu de répondre :marteau: :mur:
Sylviel
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 11 Oct 2013, 09:26
par Sylviel » 11 Oct 2013, 09:26
Encore dsl Danteo pour ma boulette. Je refais un message pour que tu voies qu'il y a eu une réponse.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 11 Oct 2013, 09:36
par Dante0 » 11 Oct 2013, 09:36
Sylviel a écrit:Encore dsl Danteo pour ma boulette. Je refais un message pour que tu voies qu'il y a eu une réponse.
Pas de problème. :lol3:
Pour le dernier terme tu fais
(x-a)²+(x-a)²+...+(x-a)² avec n termes, donc cela te donne n*(x-a)² que tu divise par n
Ah mais c'est applicable à toutes les sommes du coup non ? Vu qu'on divise par n à chaque fois ..?
Pour le terme du milieu c'est de la factorisation toute simple :
a x1 + a x2 + ... + a xn = a (x1 + x2 + ... + xn)
Je ne saisis pas trop, on factorise quoi exactement pour faire "sortir" l'expression
)
de la somme ? Je ne comprends pas trop l'utilité d'ailleurs, à mon sens c'est pas tellement une simplification. Pourquoi garder
])
sous la somme ?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 11 Oct 2013, 09:44
par Sylviel » 11 Oct 2013, 09:44
Tu ne vois pas la différence entre
(x-1)+(x-4)+(x-5)+(x-3)
et
(x-1)+(x-1)+(x-1)+(x-1) ?
Et bien c'est la même chose entre
)
et
)
Dans un cas les termes sont constants et on peut factoriser dans l'autre ils dépendent de i.
Pour l'autre terme je te conseille d'écrire explicitement ce qui se passe (pou n=3, ou avec des ...) pour comprendre. Je ne peux pas dire plus que ce que j'ai déjà écrit : chaque terme de la somme a un facteur commun (à savoir 2(\bar{X}-\alpha)) que l'on factorise (donc mets devant la somme).
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 11 Oct 2013, 10:07
par Dante0 » 11 Oct 2013, 10:07
Compris !
Sinon à la prochaine étape
^2 -2(\bar X -\alpha)^2 +(\bar X -\alpha)^2)
d'ou vient le
^2)
il est monté au carré, c'est moi qui ait fait un erreur ? (j'ai pas l'impression puisque la suite semble logique)
Ou alors c'est le fait que
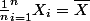
? Définition de la moyenne
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 11 Oct 2013, 10:11
par Sylviel » 11 Oct 2013, 10:11
c'est effectivement la définition de la moyenne qu'il faut utiliser :zen:
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 11 Oct 2013, 11:07
par Dante0 » 11 Oct 2013, 11:07
Sylviel a écrit:c'est effectivement la définition de la moyenne qu'il faut utiliser :zen:
Dernière question :
Pourquoi ici
= (X_i-\alpha)^2)
et
 = (\bar X -\alpha)^2)
Si on dit que alpha c'est l'espérance, normalement la formule de la variance c'est
 = E[X^2]- E[X]^2)
non ?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 11 Oct 2013, 11:50
par Sylviel » 11 Oct 2013, 11:50
Il y a deux formules (équivalentes) pour la variance.
V(X)= E((X-E(X))²)
et
V(X) = E(X²) - (E(X))²
La première est pratique pour l'intuition et la théorie, l'autre pour les calculs (en général).
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 11 Oct 2013, 18:16
par Dante0 » 11 Oct 2013, 18:16
Dacodac !
Merci ! :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
