Bonjour @aviateur : non pas du tout, j'allais d'ailleurs faire le calcul que tu as effectué et il est en cohérence avec la notion "intuitive" de statistique exhaustive.
Je ne suis pas du tout spécialiste du sujet, je n'ai que quelques notions de base mais je pense qu'elles sont suffisantes pour traiter cet exemple.
La première chose ici c'est de connaitre la définition d'une statistique exhaustive, dans le cadre du modèle paramétrique. Une statistique

est une fonction de l'échantillon
)
. Par abus de langage, on parle de statistique indifféremment pour la fonction

ou pour la v.a.
)
. Pardéfinition, une statistique

est exhaustive lorsque la loi conditionnelle de l'échantillon
)
sous

sachant

est indépendante du paramètre

.
Ensuite, on dispose d'un théorème de factorisation (j'ai vu pas mal de noms circuler suivant les bouquins : Halmos-Savage, Fisher-Neyman ) :

est exhaustive si et seulement si la vraisemblance

de l'échantillon
)
se factorise de la façon suivante : il existe des fonctions
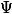
et

telles que
, \forall \theta, p_n(x_1,...,x_n;\theta) = \Psi(S(x_1,...,x_n),\theta)l(x_1,...,x_n))
En pratique, on cherche donc à calculer cette vraisemblance, et à exhiber une fonction S qui permet d'écrire une telle factorisation. Cette fonction S nous donnera alors par théorème une statistique exhaustive, sans avoir à calculer la probabilité conditionnelle.
Ce qui peut poser problème, c'est l'expression différente de cette vraisemblance dans le cas discret (mesure de comptage) et dans le cas continu (mesure de Lebesgue). Pour une v.a. discrète, la vraisemblance c'est la fonction de masse
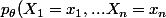)
qui est une fonction du paramètre

, étant donné les observations
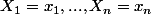
.
Pour une v.a. continue, la vraisemblance c'est la densité de probabilité
)
, étant donné une réalisation x (à dx près) de la v.a. X.
On peut, dans les deux cas, calculer l'estimateur de maximum de vraisemblance en maximisant cette fonction dérivable de

(ou plus simplement, en maximisant la log-vraisemblance, défini comme son log).
Mes connaissances s'arrêtent à peu près là, mais je voulais exposer l'exemple du modèle de Bernoulli, qui est je pense transposable ici.
Si les v.a.

sont indépendantes, de même loi, suivant toutes la loi de Bernoulli de paramètre

B(

)
=1-\theta)
,
=\theta)
, on connait la loi de
)
par produit.
La vraisemblance du modèle de Bernoulli s'écrit donc
 = \theta^{x_1+...x_n} \cdot (1-\theta)^{n-(x_1+...+x_n)} = \Psi(S(x_1,...,x_n),\theta)l(x_1,...,x_n))
avec
=x_1+...+x_n)
, et
=\theta^S(1-\theta)^{n-S})
La statistique
=X_1+...+X_n)
(à un facteur près, la moyenne empirique) est donc exhaustive.
Cette statistique était donnée, à un facteur près, par l'estimateur du maximum de vraisemblance 'EMV).
Intuitivement,

contient "toute l'information contenue sur

par l'échantillon des

". En effet, il semble naturel de supposer que l'ordre dans lequel on observe les réalisations 0 ou 1 n'apporte aucune information sur

: seul compte le nombre total de 1 dans l'échantillon.
Pour revenir à l'exercice :
- on calcule la vraisemblance du modèle
- on cherche à utiliser le théorème de factorisation
- on sait par théorème que l'estimateur du maximum de vraisemblance est une fonction de la statistique exhaustive.
- on montre que la statistique exhaustive choisie est "minimale" en un sens à préciser (toute statistique exhaustive est fonction de celle-ci)
