Stabilité et point fixe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 20 Juin 2008, 17:37
par MacManus » 20 Juin 2008, 17:37
Bonjour
On considère (de manière générale) une transformation affine f de
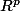
telle qu'il existe
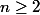
tel que
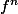
ait un point fixe A.
Soit
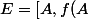,...,f^{n-1}(A)])
1. Montrer que l'ensemble E est (globalement) stable par f.
Il faut montrer que
 \subset E)
OK!
(que veut dire globalement exactement ?)
2. En déduire que f a un point fixe.
Quelqu'un peut-il m'aider pour cette dernière question?
merci beaucoup

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 20 Juin 2008, 17:56
par leon1789 » 20 Juin 2008, 17:56
MacManus a écrit: (que veut dire globalement exactement ?)
ca veut dire que f(E) est inclus dans (ou égal à) E : on parle de E globalement, et non pas point par point f(x) = x.
MacManus a écrit:2. En déduire que f a un point fixe.
tu prends

points du plan, tu les fais "tourner" sur eux-mêmes : il y a un autre point du plan qui lui n'a pas bougé. Lequel ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 20 Juin 2008, 18:00
par leon1789 » 20 Juin 2008, 18:00
mon indication n'est pas terrible... :hum:
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 20 Juin 2008, 18:14
par MacManus » 20 Juin 2008, 18:14
Merci léon1789
je comprend intuitivement ton explication. On "s'aperçoit" que le point A est invariant par f. Mais je ne parviens pas à montrer clairement (mathématiquement) que tel est le cas !
-
sclormu
- Membre Naturel
- Messages: 36
- Enregistré le: 16 Juin 2008, 10:23
-
 par sclormu » 20 Juin 2008, 18:23
par sclormu » 20 Juin 2008, 18:23
MacManus a écrit:Merci léon1789
je comprend intuitivement ton explication. On "s'aperçoit" que le point A est invariant par f. Mais je ne parviens pas à montrer clairement (mathématiquement) que tel est le cas !
C'est pas vraiment A qui ne bouge pas....
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 20 Juin 2008, 18:28
par MacManus » 20 Juin 2008, 18:28
Ah je crois comprendre un peu plus. Comme f est affine, elle préserve le barycentre. Donc si G est le barycentre de l'ensemble E, f(G) est le barycentre de f(E), cad dire f(G) barycentre de E lui-même puisque E stable par f. Donc G = f(G). le barycentre G est un point invariant par f. On peut dire ça ??
-
sclormu
- Membre Naturel
- Messages: 36
- Enregistré le: 16 Juin 2008, 10:23
-
 par sclormu » 20 Juin 2008, 19:16
par sclormu » 20 Juin 2008, 19:16
MacManus a écrit:Ah je crois comprendre un peu plus. Comme f est affine, elle préserve le barycentre. Donc si G est le barycentre de l'ensemble E, f(G) est le barycentre de f(E), cad dire f(G) barycentre de E lui-même puisque E stable par f. Donc G = f(G). le barycentre G est un point invariant par f. On peut dire ça ??
Clairement. Ceci dit il te faudra montrer que f(E)=E et pas seulement l'inclusion. Ceci dit, c'est trivial.
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 20 Juin 2008, 20:44
par MacManus » 20 Juin 2008, 20:44
eh bien on a montré que E est stable par f, cad f(E) inclu dans E. Clairement E est inclu dans f(E). Donc f(E) = E. Cependant comment montrer que f préserve le barycentre G pour l'ensemble E ?? il suffit juste de dire que f(E)=E ou il faut le démontrer ? Si c'est le cas je veux bien de l'aide.
merci à vous
-
sclormu
- Membre Naturel
- Messages: 36
- Enregistré le: 16 Juin 2008, 10:23
-
 par sclormu » 21 Juin 2008, 00:28
par sclormu » 21 Juin 2008, 00:28
MacManus a écrit:eh bien on a montré que E est stable par f, cad f(E) inclu dans E. Clairement E est inclu dans f(E). Donc f(E) = E. Cependant comment montrer que f préserve le barycentre G pour l'ensemble E ?? il suffit juste de dire que f(E)=E ou il faut le démontrer ? Si c'est le cas je veux bien de l'aide.
merci à vous
Pose
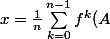)
et étudie f(x) (évidemment, il faut savoir ce qu'est une application affine.)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
