Sphère épointée

[Nightmare]

Salut à tous :happy3:

Dans le cadre d'un DM j'ai un exercice plutôt ardu à résoudre. Voici son énoncé :

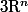
On se place dans muni de la norme euclidienne.

1) Soient A et B deux points de la boule unité ouverte, montrer qu'il existe un homéomorphisme de la boule unité fermée dans elle même qui envoie A sur B et fixe les points de la sphère unité.

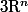
2) Soient F un fermé de complémentaire connexe et deux points A et B qui ne sont pas dans F. Montrer qu'il existe un homéomorphisme de dans lui même qui envoie A sur B et fixe les points de F.

3) Application : Montrer que si A et B sont deux sous-ensembles à n points de la sphère unité de l'espace, alors

Alors je bloque déjà pour le 1).

Déjà, on peut se ramener au cas où A=O. En indication, on nous propose de poser avec

Il est clair qu'elle est continue et par compacité de la boule unité, il me suffit de prouver qu'elle est bijective pour montrer que c'est un homéomorphisme. Problème, je n'arrive pas à montrer qu'elle est bijective. J'ai abandonné l'idée de passer par un calcul d'antécédent qui ne semble mener à rien et j'ai plutôt en tête d'essayer de trouver sa réciproque, sauf que j'ai beau chercher je ne vois pas à quoi elle peut ressembler ! Avez-vous une idée?

Merci :happy3:

[alavacommejetepousse]

bonjour
je ne comprends pas d après l énoncé l homéo n est pas défini sur la sphère

[Nightmare]

bonjour
je ne comprends pas d après l énoncé l homéo n est pas défini sur la sphère

Oui désolé je corrige ça, il faut inverser !

[alavacommejetepousse]

oui il suffit d écrire

m ' = m + tb avec t qui dépend de llmll
d'où m = m' -tb et de calculer llmll^2 en fonction de m ' et b pour avoir une équation du second degré en t dont on ne garde que la solution du bon signe

[Nightmare]

Salut !

Bon en fait j'ai trouvé en m'aidant un peu de ce que tu as proposé.

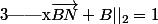
Soit N un point de la boule (qui n'est pas le pôle nord), je pose f(N) l'intersection de (BN) et de la sphère. On montre comme tu le proposes que l'équation admet une unique solution notée .

Je montre alors que si N différent de B et O sinon.

En utilisant le théorème de recollement fermé et le 1) j'ai montré de même que si B et C étaient deux points de la boule fermée centrée en A de rayon r quelconque alors il existe un homéomorphisme de R^n dans lui même qui envoie B sur C et fixé le complémentaire de la boule. Ca devrait m'aider pour le 2)

Je continue à réfléchir au sujet, merci de ton aide :happy3: