je crois que je l ai.Sans trop rentrer dans les détails:soit xn->x avec sp(xn) connexe(original comme début hein lol).Supposons que K=sp(x) puisse s écrire come union de 2 compacts disjoints
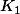
et
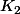
.J agrandis ces 2 compacts:
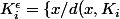\}\leq\epsilon)
avec

assez petit pour que

et

restent disjoints.Pour tout n assez grand,sp(xn) sera inclu dans l un des 2

.Quitte a extraire une sous suite de xn,et a éventuellement intervertir
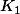
et
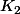
,je suppose que pour tout n,le spectre de xn est inclus dans

.On peut aussi supposer que 0 est dans K1.Soit

un cycle(=union de lacets) dans

,tel que

soit égale a 1 sur K1.En particulier,

ne rencontre aucun spectre.A n fixé appliquons la formule de Cauchy a
=\frac{1}{x_n-ze})
.On a
=\frac{1}{2i\pi}\int_\gamma \frac{f(z)}{z}dz)
donc
}dz)
Comme

ne rencontre pas le spectre de x,on en déduit que le terme de droite converge.On a donc que 1/xn converge,donc que x est inversible,absurde..
est fermé dans A
