Sous-groupes de Dn (n<=8) et de S3 [Licence]

[remjg]

Bonjour!

C'est complètement désespéré que je viens demander conseil sur ce site pour préparer un exercice de théorie des groupes.

En voici l'énoncé :
1) Etudier les sous-groupes de Dn pour n<=8 (lesquels sont distingués).
2) Etudier les sous-groupes de S3 (lesquels sont distingués).

J'aimerais connaitre la méthode pour résoudre cet exercice... Etant complètement largué depuis plusieurs semaines en algèbre, je ne sais même pas comment m'y prendre!

Merci d'avance!

PS : Dn est le groupe diédral (isométries laissant invariant un n-gone régulier) et S3 le groupe des permutations d'un ensemble a 3 éléments.

[yos]

Dans 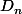, il y a n symétries et n rotations (dont l'identité). Soit G un sous-groupe de 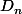. Si G ne contient que des rotations, c'est un sous-groupe du groupe cyclique .
S'il contient une symétrie et pas de rotation, c'est (une autre symétrie fournirait une rotation par composition avec la première). Avec au moins une symétrie et au moins une rotation, on tombe sur un 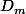avec .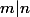
Ma classification est sûrement pas optimale mais c'est une façon d'attaquer le problème.

[remjg]

Merci pour vous réponses à tous les 2! Ca va m'éviter d'avancer dans l'inconnu ;)
Pour l'instant j'apprend mon cours...

J'ai déjà malgré tout penché sur S3 et je trouve la même chose (la table de la loi est facile a écrire et facilite pas mal les choses).

Je me réserve Dn pour la fin, je déteste ce groupe...

Enfin, si vous avez d'autres indications à me donner n'hésitez pas! Je n'ai pas le temps de répondre mais je vous lis ;)

[Joker62]

Tiens ils en parlent un peu là dessus
http://pagesperso-orange.fr/serge.hublau/006_groupes_diedraux.pdf

[ThSQ]

Les diédraux :

D_1 : facile ;) Z/2Z

D_2 : c'est Z/2Z x Z/2Z, commutatif, 3 sous-groupes isomorphes (forcément distingués)

D_3 : non-abélien, c'est S_3 traité juste avant

D_4 : non-abélien.
Ca devient sportif. Le sous-groupes sont Z/2Z (y'en a 5 je crois, les éléments d'ordre 2), Z/4Z (1?), distingués et Z/2Z x Z/2Z, distingué.
Regarder si les Z/2Z sont distingués est au-delà de mes forces mais au pif je dirais que non.

Je sais pas si ça t'aide.

D_5 .. D_8 : là c'est inhumain.

[ThSQ]

J'espère qu'on me pardonnera ce petit "up" afin de savoir si remjg a eu des éléments de réponses pour D_n.

[remjg]

J'espère qu'on me pardonnera ce petit "up" afin de savoir si remjg a eu des éléments de réponses pour D_n.

Je posterai dans la semaine la correction
Ca ne s'est pas très bien passé pour moi au tableau donc il faut que je prenne le temps de revoir tout ca! Ah les maths...

[ThSQ]

Je posterai dans la semaine la correction

Ok Merci !

Vous avez fait tous les D_n jusqu'à 8 ???