Sous Groupes additifs
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 04 Juin 2007, 14:38
par mehdi-128 » 04 Juin 2007, 14:38
Bonjour,on considère le sous groupe additif engendré par a et b:
G(a,b)={na+mb,n et m dans Z}
Montrer que G(a,b) discret si et seulement si:a/b appartenant a Q.
Dans ce cas,on montrera que si: / (a/b) /=(p/q) avec p et q dans N et p et q premiers entre eux,le sous groupe:G(a,b)=(a/p)Z
Je comprends pas grand chose ,merci.....
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 04 Juin 2007, 14:46
par aviateurpilot » 04 Juin 2007, 14:46
j'ai vu la definition de discret dans google pour avoir pouvoir resoudre cet exo
)
discret
donc
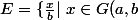\}=Z+\frac{a}{b}Z)
discret.
mtn l'exo est tres facile
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 04 Juin 2007, 15:04
par mehdi-128 » 04 Juin 2007, 15:04
c'est quoi E ?
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 04 Juin 2007, 15:07
par aviateurpilot » 04 Juin 2007, 15:07
mehdi-128 a écrit:c'est quoi E ?
c'est l'ensemble des element de G divisé par b.
par exemple si G={1,2,3,4...}
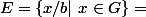
{1/b , 2/b , 3/b....}
c'est quoi discret d'apres ton cours?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 04 Juin 2007, 15:45
par mehdi-128 » 04 Juin 2007, 15:45
Discret c'est de la forme aZ ou a apartient a R.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 04 Juin 2007, 15:49
par mehdi-128 » 04 Juin 2007, 15:49
Oui mais y a équivalence......
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 04 Juin 2007, 15:54
par aviateurpilot » 04 Juin 2007, 15:54
donc on peux montrer facilement
que G discret ssi E={x/b avec x dans G} l'est aussi
et c'et ce que j'ai fait.
il suffit mtn de montrer que (1): Z+(a/b)Z discret ssi (2):a/b dans Q
2=>1 evidant
il te rest 1=>2.
x=a/b
donc tu doi montrer que x irrationnel =>

-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 04 Juin 2007, 16:21
par yos » 04 Juin 2007, 16:21
Bonjour.
C'est sûrement redondant avec ce que t'a fait aviateurpilote mais ça peut t'aider.
1) si G(a,b) discret, G=rZ, donc
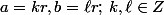
, donc
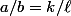
, donc a/b rationnel.
2) Réciproque : a/b rationnel donc
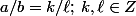
et on peut supposer
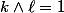
.
On a donc
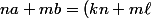a/k)
donc
 \subset (a/k)Z)
.
Pour l'autre inclusion, il suffit de prouver que
)
; pour ça on peut partir de Bézout :
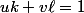
donc
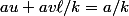
, donc
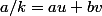
donc

-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
 par Lierre Aeripz » 04 Juin 2007, 16:35
par Lierre Aeripz » 04 Juin 2007, 16:35
Petit complément classique... On peut se demander ce qui se passe si a/b n'est pas rationnel.
Soit
\in{\mathbb{R}^*_+}^2)
.
Montrons que

est dense dans \mathbb{R} si

et est monogène sinon.
On note
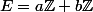
.
On pose
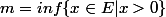
.
1er cas. 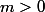
Alors
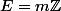
.
En effet, soit

. Soit

tel que

.

et

. Par définition de m,
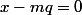
.
Donc

.
Donc
 2nd cas.
2nd cas. 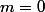
Montrons que E coupe tout ouvert de

.
Soit
 \in \mathbb{R}^2, 0 < u < v)
(C'est pareil si on change les signes.)
Comme
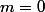
,

.

.
Dans

car

et dans E car

.
Donc E dense dans

.
-
Daniel-Jackson
- Membre Relatif
- Messages: 160
- Enregistré le: 19 Mai 2007, 17:49
-
 par Daniel-Jackson » 04 Juin 2007, 16:42
par Daniel-Jackson » 04 Juin 2007, 16:42
C'est exactement ce que dit le théorème de classification des sous groupes additifs de R :
Un sous groupe de R est soit dense , soit discret . S'il est discret il est de la forme aZ .
Il y'a plusieurs démonstartions dont celle donnée par Lierre Aeripz
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 04 Juin 2007, 16:45
par mehdi-128 » 04 Juin 2007, 16:45
Ok merci yos.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 04 Juin 2007, 16:48
par mehdi-128 » 04 Juin 2007, 16:48
Une autre question:En admettant que Pi est irrationnel en considérant G(1,2Pi) et le fait que cos est surjective de R sur [-1,1] en déduire l'ensemble des valeurs d'adhérence de la suite (cos(n)).
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 04 Juin 2007, 16:52
par aviateurpilot » 04 Juin 2007, 16:52
Yos a écrit:C'est sûrement redondant avec ce que t'a fait aviateurpilote mais ça peut t'aider.
mais je viens de voir la definition de cet notion (discret).
si x=a/b irrationnel,
il existe une suite
)
qui converge vers x
on a donc

converge vers

donc

n'est pas discret
-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
 par Lierre Aeripz » 04 Juin 2007, 16:53
par Lierre Aeripz » 04 Juin 2007, 16:53
 = cos(x))
Avec ceci, et la densité dans

de

tu devrais y arriver seul.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 04 Juin 2007, 16:57
par mehdi-128 » 04 Juin 2007, 16:57
désolé mais je vois pas le rapport entre G(1,2Pi) et la suite cos(n).....
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 04 Juin 2007, 16:59
par aviateurpilot » 04 Juin 2007, 16:59
mehdi-128 a écrit:désolé mais je vois pas le rapport entre G(1,2Pi) et la suite cos(n).....
|\ n\in N\}=\{cos(x)|\ x\in G(1,2\pi)\}\ dense\ dans\ cos(\mathbb{R}))
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 04 Juin 2007, 17:01
par yos » 04 Juin 2007, 17:01
aviateurpilot a écrit:mais je viens de voir la definition de cet notion (discret).
Non mais j'ai pas critiqué ton truc.
Redondant ça veut dire que c'est la même chose.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 04 Juin 2007, 17:02
par aviateurpilot » 04 Juin 2007, 17:02
yos a écrit:Non mais j'ai pas critiqué ton truc.
Redondant ça veut dire que c'est la même chose.
je uis tres nul en francais :ptdr:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 04 Juin 2007, 17:03
par yos » 04 Juin 2007, 17:03
)
dense dans R donc son image par la fonction cosinus (qui est continue) est ...
-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
 par Lierre Aeripz » 04 Juin 2007, 17:03
par Lierre Aeripz » 04 Juin 2007, 17:03
 \in (\mathbb{Z}^\mathbb{N})^2, p_n - 2q_n\pi \to a \text{et} p_n - 2q_n\pi \neq a)
On montre que

.
Tu vois ou je continue ?
Utilisateurs parcourant ce forum : Fulano et 90 invités
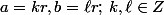 , donc
, donc 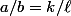 , donc a/b rationnel.
, donc a/b rationnel.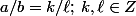 et on peut supposer
et on peut supposer 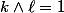 .
.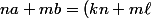a/k) donc
donc  \subset (a/k)Z) .
.) ; pour ça on peut partir de Bézout :
; pour ça on peut partir de Bézout : 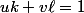 donc
donc 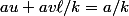 , donc
, donc 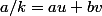 donc
donc 
\in{\mathbb{R}^*_+}^2) .
. est dense dans \mathbb{R} si
est dense dans \mathbb{R} si  et est monogène sinon.
et est monogène sinon.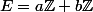 .
.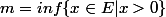 .
.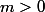
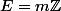 .
. . Soit
. Soit  tel que
tel que  .
. et
et  . Par définition de m,
. Par définition de m, 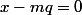 .
. .
.
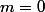
 .
. \in \mathbb{R}^2, 0 < u < v) (C'est pareil si on change les signes.)
(C'est pareil si on change les signes.)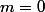 ,
,  .
. .
. car
car  et dans E car
et dans E car  .
. .
.