Sous Groupes additifs
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
 par Lierre Aeripz » 04 Juin 2007, 17:05
par Lierre Aeripz » 04 Juin 2007, 17:05
Moui c'est vrai... Autant utiliser le résultat sous la forme proposé par AP.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 04 Juin 2007, 17:13
par yos » 04 Juin 2007, 17:13
aviateurpilot a écrit:je uis tres nul en francais :ptdr:
ça équilibre avec les maths.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 04 Juin 2007, 17:17
par mehdi-128 » 04 Juin 2007, 17:17
\forall a \in \mathbb{R}, \exists ( p, q ) \in (\mathbb{Z}^\mathbb{N})^2, p_n - 2q_n\pi \to a \text{et} p_n - 2q_n\pi \neq a
On montre que p_n \to \infty.
je comprends pas grand chose;pour ne pas dire rien...
-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
 par Lierre Aeripz » 04 Juin 2007, 17:24
par Lierre Aeripz » 04 Juin 2007, 17:24
L'idée est de montrer que
_{n\in\mathbb{N}})
admet tous les réels de [0, 2\pi[ comme valeur d'adhérence. Donc que
 )_{n\in\mathbb{N}})
admet tous les réels de [-1, 1] comme v.a..
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 04 Juin 2007, 17:27
par aviateurpilot » 04 Juin 2007, 17:27
j'ai deja ecris ça
|\ n\in N\}=\{cos(x)|\ x\in G(1,2\pi)\}\ dense\ dans\ cos(\mathbb{R})=[-1,1])
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 04 Juin 2007, 17:29
par mehdi-128 » 04 Juin 2007, 17:29
Ah sous cette forme je comprends mieux merci....
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 05 Juin 2007, 12:04
par aviateurpilot » 05 Juin 2007, 12:04
mehdi-128 a écrit:Ah sous cette forme je comprends mieux merci....
je t'ai dit
))
dense dans
)
mais t'ai pas montrer que
)
est dense dans
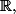
tu veux que je le fait?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 05 Juin 2007, 12:33
par mehdi-128 » 05 Juin 2007, 12:33
ouai je veux bien....
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 05 Juin 2007, 12:36
par mehdi-128 » 05 Juin 2007, 12:36
Il faut montrer que pour tout x appartenant a R ,il existe une suite (an) de G(1,2Pi) tel que : lim(an)=x.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 05 Juin 2007, 12:52
par aviateurpilot » 05 Juin 2007, 12:52
il existe une suite
\in \mathbb{Q}^{\mathbb{N}})
qui converge vers

avec
\in \mathbb{N}^2)
on a donc
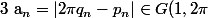-\{0\})
converge vers

N.B
\in Z\times N,\ ka_n\in G(1,2\pi)
)
mtn soit

et soit

.
\cap G(1,2\pi)\neq \empty)
soit
)
une suite de G(1,2pi) tel que
\cap G(1,2\pi))

-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 05 Juin 2007, 15:39
par mehdi-128 » 05 Juin 2007, 15:39
Y a 2 trucs que je comprends pas :
il existe une suite 3$ (\frac{p_n}{q_n})\in \mathbb{Q}^{\mathbb{N}} qui converge vers 3$ 2\pi
et donc 3$ \exist (b,k)\in [0,a_{n_0}[\times Z,\ x=b+ka_{n_0}
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 05 Juin 2007, 16:44
par aviateurpilot » 05 Juin 2007, 16:44
mehdi-128 a écrit:Y a 2 trucs que je comprends pas :
il existe une suite 3$ (\frac{p_n}{q_n})\in \mathbb{Q}^{\mathbb{N}} qui converge vers 3$ 2\pi
et donc 3$ \exist (b,k)\in [0,a_{n_0}[\times Z,\ x=b+ka_{n_0}
il existe une suite
\in \mathbb{Q}^{\mathbb{N}})
qui converge vers

Q est dense dans R
donc il existe une suite sur Q qui converge vres

là c'est comme la congruenece dans

soit
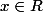
et

on pose
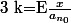\ et\ b=x-ka_{n_0})


donc
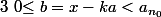
et comme tu vois, on a bien
\in [0,a_{n_0}[\times Z,)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 05 Juin 2007, 17:08
par mehdi-128 » 05 Juin 2007, 17:08
Ah ok merci,bien joué :)...
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 05 Juin 2007, 17:10
par aviateurpilot » 05 Juin 2007, 17:10
mehdi-128 a écrit:Ah ok merci,bien joué

...
de rien :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
qui converge vers

