Sous espace vectoriel + famille libre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 01 Juin 2021, 18:08
par novicemaths » 01 Juin 2021, 18:08
Bonsoir
Je souhaiterais une correction de l'exercice ci-dessous.
On considère les vecteurs  ,
,  ,
,  . Montrer que
. Montrer que  ,
,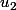 ,
,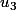 forment
forment
une famille libre de vecteurs. En déduire que le sous-espace vectoriel de  engendré par
engendré par  ,
,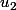 ,
,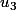 égal à
égal à 

.
On vérifie que la famille est libre.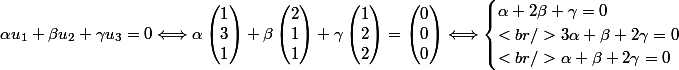
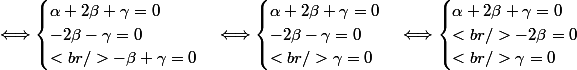
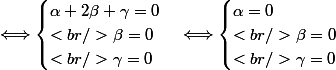
La famille des vecteurs

,
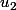
,
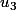
est bien libre.
On vérifie que la famille est génératrice.
et


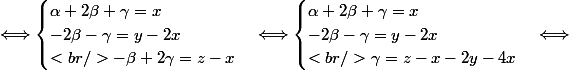
 =y-z\\<br />\gamma = z-5x-2y<br />\end{cases} \Longleftrightarrow \begin{cases} <br />\alpha + 2\beta + \gamma =x\\<br />-2 \beta =5x -3y\\<br />\gamma = z-5x-2y<br />\end{cases} \Longleftrightarrow)
 + (z-5x-2y) =x\\<br />\beta =-\frac{5}{2}x + \frac{3}{2}y\\<br />\gamma = z-5x-2y<br />\end{cases} \Longleftrightarrow)
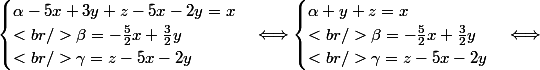
 Je sais il y a trop de calcul, mais je ne vois pas comment démontrer autrement que c'est un sous espace vectoriel de dimension 3
Je sais il y a trop de calcul, mais je ne vois pas comment démontrer autrement que c'est un sous espace vectoriel de dimension 3
De plus, pourriez-vous me dire si le calcul de la famille génératrice est correct ?.
Pars avance, merci !!!
A bientôt
-
azf
 par azf » 01 Juin 2021, 18:28
par azf » 01 Juin 2021, 18:28
novicemaths a écrit:
[color=#800080]Je sais il y a trop de calcul, mais je ne vois pas comment démontrer autrement que c'est un sous espace vectoriel de dimension 3
Bonjour
Pourquoi tous ces calculs?
le déterminant donne -6
si c'est juste pour savoir si les trois vecteurs engendrent R^3 et forment une famille libre
alors vous avez une matrice carrée inversible (donc de déterminant non nul)
-
azf
 par azf » 01 Juin 2021, 18:44
par azf » 01 Juin 2021, 18:44
depuis que je regarde vos sujets je dois vous avouer un truc : je ne lis jamais vos calculs et un jour c'est comme l'histoire de celui qui criait au loup , il sera important de lire vos calculs et là je passerai à côté : c'est bien triste tout ça!
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 01 Juin 2021, 18:45
par novicemaths » 01 Juin 2021, 18:45
Ah il faut juste faire le calcul de déterminant
Dans mon livre, il montre ces calculs pour les sous espaces vectoriel (famille libre et génératrice).
Merci !
A bientôt.
-
azf
 par azf » 01 Juin 2021, 19:03
par azf » 01 Juin 2021, 19:03
novicemaths a écrit:
Dans mon livre, ...
Ah oui j'oubliais qu'on fait pareil nous ... c'est vrai que c'est pas évident
Bon courage à vous!!
Pensez aussi à voir "rang d'une matrice"
transformation élémentaires sur les matrices
c'est important pour quand vous verrez les diagonalisations
bref .... bref.... bref... de toute façon c'est une question de vie ou de mort (on n'a pas le choix )
-
azf
 par azf » 01 Juin 2021, 19:16
par azf » 01 Juin 2021, 19:16
azf a écrit:bref .... bref.... bref... de toute façon c'est une question de vie ou de mort (on n'a pas le choix )
oui ça commence : déjà un mort tué par un drone d'une armée qui a pris la décision tout seul d'abattre un pauvre civil qui faisait son jogging tranquillos
c'est clair qu'on n'a pas le choix
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 01 Juin 2021, 22:15
par novicemaths » 01 Juin 2021, 22:15
Merci azf !
J'aurais souhaité savoir si mes calculs sont corrects.
A bientôt
-
azf
 par azf » 02 Juin 2021, 07:06
par azf » 02 Juin 2021, 07:06
novicemaths a écrit:Ah il faut juste faire le calcul de déterminant
Ici oui puisque qu'on vous demande juste d'une part s'ils génèrent l'espace
et d'autre part s'il forment une famille libre
Entrainez-vous à la main
Quel est le déterminant de

?
Avez-vous vu la signature d'une permutation?
123(+)

on va dans l'ordre
132(-)

on inverse les deux derniers
213(-)

on va dans l'ordre
231(+)
on inverse les deux dernier
312(+)
on va dans l'ordre
321(-)
on inverse les deux derniers
_______________________
1234(+)
1243(-)
1324(-)
1342(+)
etc... +--++--++--++--++--++--++-- etc...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
