[MPSI] sommes et intégrales
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 20 Jan 2007, 14:21
par pouik » 20 Jan 2007, 14:21
Bonjour,
J'ai quelques soucis avec ces trois question donc si vous pouviez mp'aider ce serait vraiment genial :we: . Merci d'avance.
1.(a) Calculer, pour tout

, la somme

.
(b) Mettre le résultat sous la forme :
t\right)}{2\sin{\frac{t}{2}}} - \lambda)
, ou

est une constante que l'on déterminera.
2. Etablir, pour tout
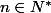
, l'égalité :
 = \displaystyle\int_{0}^{\pi} \phi(t) \sin\left(\left(n+\frac{1}{2}\right)t\right) dt - \frac{1}{2} \displaystyle\int_{0}^{\pi} \left(\frac{t^2}{2\pi} - t\right) dt)
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 20 Jan 2007, 14:23
par fahr451 » 20 Jan 2007, 14:23
bonjour
1a) coskt = Re ( exp(ikt) ) et utilise la somme de termes d'une suite géométrique
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 20 Jan 2007, 14:27
par pouik » 20 Jan 2007, 14:27
Pour la 1. (a) je propose :
# On a :
)
c'est-à-dire :
)
c'est-à-dire d'après la
formule de Moivre :
)
## Calculons
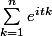
.
On reconnait la somme des

termes consécutifs d'une suite géométrique de raison
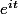
;
d'où :
-
1er cas : si
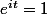
, c'est-à-dire si

;
alors :
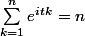
donc :
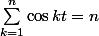
-
2ème cas : si

, c'est-à-dire si

;
alors :
^n}{1 - e^{it})
c'est-à-dire :
}{1 - e^{it}})
c'est-à-dire :
x} [-2i\sin{\left(\left(\frac{n}{2}\right)t\right)}]}{e^{i(\frac{t}{2})} \left[-2i\sin{\left(\frac{t}{2}\right)}\right]})
c'est-à-dire :
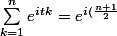t} \frac{\sin{\left(\left(\frac{n}{2}\right)t\right)}}{\sin{\left(\frac{t}{2}\right)}})
D'où, en prenant la
partie réelle :
}{2}t}\right) \left(\sin{\left(\left(\frac{n}{2}\right)t\right)}\right)}{\sin{\left(\frac{t}{2}\right)}})
Est-ce correct ?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 20 Jan 2007, 14:32
par fahr451 » 20 Jan 2007, 14:32
oui mais ce n'est pas sous la forme demandée .
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 20 Jan 2007, 14:58
par pouik » 20 Jan 2007, 14:58
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 20 Jan 2007, 15:34
par yos » 20 Jan 2007, 15:34
pouik a écrit:c'est-à-dire d'après la
formule de Moivre :
)
Le k porte sur
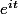
et pas sur la somme.
Ensuite c'est plutôt sina cosb=1/2[sin(a+b)+sin(a-b)].
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 20 Jan 2007, 15:45
par pouik » 20 Jan 2007, 15:45
non je suis d'accord pour le k : en fait si on regarde attentivement le k est bien avant la paranthèse, c'est le Latex qui donne l'impression contraire.
Sinon pour :
sina cosb=1/2[sin(a+b)+sin(a-b)]
Je ne vois pas ce qu'il faut poser pour a et b !
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 20 Jan 2007, 15:46
par fahr451 » 20 Jan 2007, 15:46
comme quoi le latex est pervers
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 20 Jan 2007, 15:58
par yos » 20 Jan 2007, 15:58
a=nt/2, b=(n+1)t/2
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 20 Jan 2007, 16:28
par pouik » 20 Jan 2007, 16:28
donc :
}{2}t} + \sin{-\frac{t}{2}} \right)}{\sin{\left(\frac{t}{2}\right)}})
Est-ce correct ?
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 20 Jan 2007, 20:26
par pouik » 20 Jan 2007, 20:26
pouvez-vous me dire si c'est correct ?
Merci d'avance.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 20 Jan 2007, 21:59
par yos » 20 Jan 2007, 21:59
C'est bon. Une simplification et tu as la forme demandée.
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 20 Jan 2007, 22:13
par pouik » 20 Jan 2007, 22:13
comme
 = -\sin(x))
on en déduit que
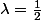
Non ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 20 Jan 2007, 22:24
par yos » 20 Jan 2007, 22:24
Oui c'est ça.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités